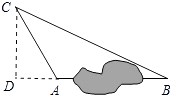
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
参考答案:
【答案】解:过点C作CD⊥AB于D,如图所示:
在Rt△CDA中,∠CAD=180°∠CAB=180°120°=60°
∵sin∠CAD= ![]() ,
,
∴CD=ACsin60°=50× ![]() =25
=25 ![]() (m),
(m),
同理:AD=ACcos60°=50× ![]() =25(m),
=25(m),
在Rt△CBD中,BD= ![]() =25
=25 ![]() (m)
(m)
∴AB=BDAD=25 ![]() 25(m),
25(m),
答:AB之间的距离是(25 ![]() -25)m.
-25)m.
【解析】通过做三角形的高,将要求的问题转化到直角三角形中求解,因此过点C作CD⊥AB于D,在Rt△CDA求出∠CAD的度数,再利用锐角函数的定义求出CD的长,然后在Rt△CBD中,利用勾股定理求出BD的长,最后根据AB=BDAD,计算得出结果即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
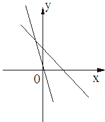 B.
B. 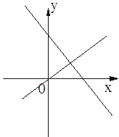
C.
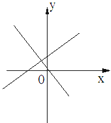 D.
D. 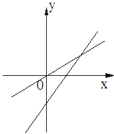
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52.根据上面四式的计算规律求:1+2+3+…+2014+2015+2016+2015+2014+…+3+2+1=________(写出某数的平方即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读并填空:
已知:如图,∠1=∠2,∠C=∠D,试说明:∠A=∠F.

解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠3(等量代换)
∴BD∥EC( )
∴∠4=∠C(两直线平行,同位角相等)
又∠C=∠D(已知)
∴∠4=∠D( )
∴ ∥ (内错角相等,两直线平行)
∴∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.

(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.

(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.

(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
相关试题

