【题目】认真阅读并填空:
已知:如图,∠1=∠2,∠C=∠D,试说明:∠A=∠F.

解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠3(等量代换)
∴BD∥EC( )
∴∠4=∠C(两直线平行,同位角相等)
又∠C=∠D(已知)
∴∠4=∠D( )
∴ ∥ (内错角相等,两直线平行)
∴∠A=∠F( )
参考答案:
【答案】(对顶角相等),(同位角相等,两直线平行),(等量代换),DF,AC,(两直线平行,内错角相等)
【解析】
先求出∠1=∠3,推出BD∥EC,根据平行线的性质推出∠C=∠D=∠4,根据平行线的判定推出DF∥AC即可.
∵∠1=∠2(已知),∠2=∠3(对顶角相等),
∴∠1=∠3(等量代换),
∴BD∥EC(同位角相等,两直线平行),
∴∠4=∠C(两直线平行,同位角相等)
又∵∠C=∠D(已知),
∴∠4=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案为:(对顶角相等),(同位角相等,两直线平行),(等量代换),DF,AC,(两直线平行,内错角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A
 B
B C
C .
.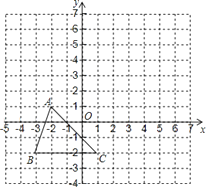
(1)在图中画出△A
 B
B C
C ;
;(2)写出点A
 、B
、B 、C
、C 的坐标;
的坐标;(3)在
 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
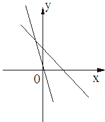 B.
B. 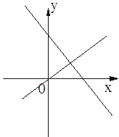
C.
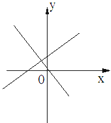 D.
D. 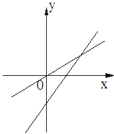
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52.根据上面四式的计算规律求:1+2+3+…+2014+2015+2016+2015+2014+…+3+2+1=________(写出某数的平方即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.

(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.

(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
相关试题

