【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).

参考答案:
【答案】(1)轿车到达乙地后,货车距乙地30千米;
(2)CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);
(3)货车从甲地出发约4.68小时后再与轿车相遇.
【解析】试题分析:(1)本题求出货车与轿车的速度是解题的关键.根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时,再根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米;(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解;(3)设货车从甲地出发x小时后再与轿车相遇,根据轿车(x﹣4.5)小时行驶的路程+货车x小时行驶的路程=300千米列出方程,解方程即可.
试题解析:(1)根据图象信息:货车的速度V货=![]() =60(千米/时).∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).轿车到达乙地后,货车距乙地30千米;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,∴
=60(千米/时).∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).轿车到达乙地后,货车距乙地30千米;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,∴![]() ,解得
,解得![]() ,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);(3)设货车从甲地出发后x小时后再与轿车相遇.∵V货车=60千米/时,所以V轿车=
,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);(3)设货车从甲地出发后x小时后再与轿车相遇.∵V货车=60千米/时,所以V轿车=![]() =110(千米/时),∴110(x﹣4.5)+60x=300,解得x≈4.68(小时).货车从甲地出发约4.68小时后再与轿车相遇.
=110(千米/时),∴110(x﹣4.5)+60x=300,解得x≈4.68(小时).货车从甲地出发约4.68小时后再与轿车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=
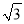 ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.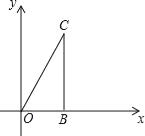
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB,根据以下作图过程:
(1)分别以点A、点B为圆心,大于AB长的
 为半径作弧,两弧相交于C、D两点;
为半径作弧,两弧相交于C、D两点;(2)过C、D两点作直线CD.
求证:直线CD是线段AB的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我县实施新课程改革后,学生的自主字习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调査了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①AD是△ABC的角平分线,则∠________=∠________=
 ∠________,
∠________,②AE是△ABC的中线,则________=________=
 ________,
________,③AF是△ABC的高线,则∠________=∠________=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=
 ,求AD的长.
,求AD的长.
相关试题

