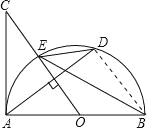
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

参考答案:
【答案】(1)AC与⊙O相切,证明参见解析;(2)![]() .
.
【解析】
试题分析:(1)由于OC⊥AD,那么∠OAD+∠AOC=90°,又∠BED=∠BAD,且∠BED=∠C,于是∠OAD=∠C,从而有∠C+∠AOC=90°,再利用三角形内角和定理,可求∠OAC=90°,即AC是⊙O的切线;(2)连接BD,AB是直径,那么∠ADB=90°,在Rt△AOC中,由于AC=8,∠C=∠BED,cos∠BED=![]() ,利用三角函数值,可求OA=6,即AB=12,在Rt△ABD中,由于AB=12,∠OAD=∠BED,cos∠BED=
,利用三角函数值,可求OA=6,即AB=12,在Rt△ABD中,由于AB=12,∠OAD=∠BED,cos∠BED=![]() ,同样利用三角函数值,可求AD.
,同样利用三角函数值,可求AD.
试题解析:(1)AC与⊙O相切.∵弧BD是∠BED与∠BAD所对的弧,∴∠BAD=∠BED,∵OC⊥AD,∴∠AOC+∠BAD=90°,∴∠BED+∠AOC=90°,即∠C+∠AOC=90°,∴∠OAC=90°,∴AB⊥AC,即AC与⊙O相切;(2)连接BD.∵AB是⊙O直径,∴∠ADB=90°,在Rt△AOC中,∠CAO=90°,∵AC=8,∠ADB=90°,cos∠C=cos∠BED=![]() ,∴AO=6,∴AB=12,在Rt△ABD中,∵cos∠OAD=cos∠BED=
,∴AO=6,∴AB=12,在Rt△ABD中,∵cos∠OAD=cos∠BED=![]() ,∴AD=ABcos∠OAD=12×
,∴AD=ABcos∠OAD=12×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】台北捷连木栅线票价及行驶时间表,如表,请问:

范例:忠孝复兴站至辛亥站之票价为25元,自科技大楼站至木栅站需时12分钟.
(1)某同学自南京东路站搭木栅线捷运电联车,欲至万芳社区站,投一枚50元硬币购买车票,应该找回几元?
(2)该同学于上午七时十分搭上电联车,应该何时到达万芳社区站?
-
科目: 来源: 题型:
查看答案和解析>>【题目】联系实际编拟一道关于分式方程
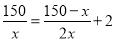 的应用题,要求表述完整,条件充分并写出解答过程。
的应用题,要求表述完整,条件充分并写出解答过程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在8×8的网格中,我们把△ABC在图1中作轴对称变换,在图2中作旋转变换,已知网格中的线段ED、线段MN分别是边AB经两种不同变换后所得的像,请在两图中分别画出△ABC经各自变换后的像,并标出对称轴和旋转中心(要求:不写作法,作图工具不限,但要保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(3x+5)2﹣(x﹣9)2=0
(2)6+3x=x(x+2). -
科目: 来源: 题型:
查看答案和解析>>【题目】一轮船在静水中的速度是30千米/小时,顺水速度是逆水速度的3倍,则水流速度 千米/小时.
相关试题

