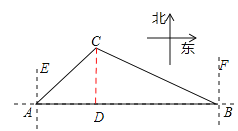
【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

参考答案:
【答案】(1)海轮在航行过程中与灯塔C的最短距离是34.4海里;
(2)海轮在B处时与灯塔C的距离约为60海里.
【解析】试题分析:(1)过点C作CD⊥AB于点D,则CD的长为海轮在航行过程中与灯塔C的最短距离.
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
试题解析:解:(1)如答图,过点C作CD⊥AB于点D,
依题意得:∠ACD=∠CAE=42°,∠BCD=∠CBF=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°=![]() ,则AD=xtan42°,
,则AD=xtan42°,
在Rt△BCD中,tan55°=![]() ,则BD=xtan55°,
,则BD=xtan55°,
∵AB=80,∴AD+BD="80." ∴xtan42°+xtan55°=80,解得:x≈34.4.
答:海轮在航行过程中与灯塔C的最短距离是34.4海里.
(2)在Rt△BCD中,cos55°=![]() ,∴BC=
,∴BC=![]() ≈60海里.
≈60海里.
答:海轮在B处时与灯塔C的距离是60海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县实施新课程改革后,学生的自主字习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调査了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①AD是△ABC的角平分线,则∠________=∠________=
 ∠________,
∠________,②AE是△ABC的中线,则________=________=
 ________,
________,③AF是△ABC的高线,则∠________=∠________=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
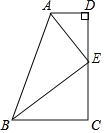
查看答案和解析>>【题目】如图,∠D=∠C=90°,点E是DC的中点,AE平分∠DAB,∠DEA=28°,求∠ABE的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2013年启动省级园林城市创建工作,计划2015年下半年顺利通过验收评审.该市为加快道路绿化及防护绿地等各项建设.在城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
相关试题

