【题目】已知在平面直角坐标系中点A(a,b),点B(a,0)的坐标满足|![]() a-b|+(a-4)2=0
a-b|+(a-4)2=0
(1)求点A、点B的坐标;
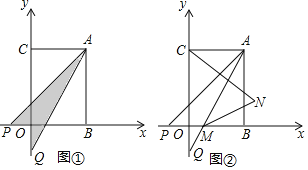
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动,同时,点Q从C点出发,沿y轴负方向以1.5个单位每秒的速度移动.某一时刻,如图①所示,且S阴=![]() S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;
(3)在(2)的条件和结论下,如图②所示,设AQ交轴于点M,作∠ACO、∠AMB的角平分线交于点N,求此时![]() 的值.
的值.
参考答案:
【答案】(1)A(4,6),B(4,0);(2)6;(3)![]() .
.
【解析】
(1)根据非负数的性质,根据方程组即可解决问题;
(2)设点P的运动时间为t秒.则BP=t,CQ=1.5t,QH=AC=4,AH=CQ=1.5t,根据S阴=S△APB+S矩形OBHQ-S△AQH,构建方程即可解决问题;
(3)由(2)可知,BP=t=6=AB,推出△ABP为等腰直角三角形,推出∠APB=45°,由CN平分∠ACQ,MN平分∠AMB,推出∠ACN=![]() ×90°=45°,∠BMN=
×90°=45°,∠BMN=![]() ∠AMB,推出∠APB=∠ACN=45°,过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB,可得∠GNM=∠NMB=
∠AMB,推出∠APB=∠ACN=45°,过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB,可得∠GNM=∠NMB=![]() ∠AMB,推出∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=
∠AMB,推出∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=![]() ∠AMB,即可得出结论.
∠AMB,即可得出结论.
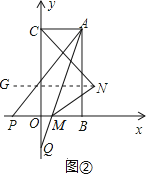
(1)∵|![]() a-b|+(a-4)2=0
a-b|+(a-4)2=0
∴|![]() a-b|≥0,(a-4)2≥0,
a-b|≥0,(a-4)2≥0,
∴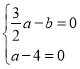 ,
,
解得![]() ,
,
∴A(4,6),B(4,0).
(2)由(1)可知,C(0,6),四边形OCAB是矩形,AC=4,AB=6,
过点Q作QH⊥AB于H.

设点P的运动时间为t秒.则BP=t,CQ=1.5t,QH=AC=4,AH=CQ=1.5t,
S阴=S△APB+S矩形OBHQ-S△AQH
=![]() ×6t+4(1.5t-6)-
×6t+4(1.5t-6)-![]() ×4×1.5t
×4×1.5t
=6t-24,
∵S阴=![]() S四边形OCAB,
S四边形OCAB,
∴6t-24=![]() ×4×6,
×4×6,
∴t=6.
(3)由(2)可知,BP=t=6=AB,
∴△ABP为等腰直角三角形,
∴∠APB=45°,
∵CN平分∠ACQ,MN平分∠AMB,
∴∠CN=![]() ×90°=45°,∠BMN=
×90°=45°,∠BMN=![]() ∠AMB,
∠AMB,
∴∠APB=∠ACN=45°,
过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB
∵AC∥x轴,NG∥x轴,
∴∠GNM=∠NMB=![]() ∠AMB,
∠AMB,
∴∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=![]() ∠AMB,
∠AMB,
∴![]() =
=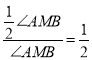 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣
 ≤x<n+
≤x<n+  ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题: (1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]=
 x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为____________海里/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 (a≥0),给出下列说法:
(a≥0),给出下列说法:
①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a> ;
;
③不论a取什么实数,2x+y的值始终不变;
④某直角三角形的两条直角边长分别为x+y,x﹣y,则其面积最大值为 .
.
以上说法正确的是( )
A.②③
B.①②④
C.③④
D.②③④
相关试题

