【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿对角线
出发,沿对角线![]() 向点
向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,使得点
,使得点![]() 落在射线
落在射线![]() 上.点
上.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,以
,以![]() 为圆心,
为圆心,![]() 半径作
半径作![]() .点
.点![]() 与点
与点![]() 同时出发,设它们的运动时间为
同时出发,设它们的运动时间为![]() (单位:
(单位:![]() )
)![]() .
.
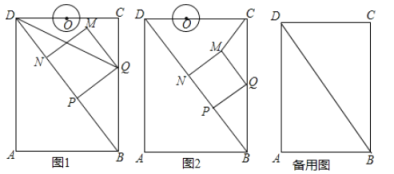
(1)如图1,连接![]() ,若
,若![]() 平分
平分![]() ,则
,则![]() 的值为__________
的值为__________![]() ;
;
(2)如图2,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 关于t的函数关系式;
关于t的函数关系式;
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 与
与![]() 第一次相切?
第一次相切?
参考答案:
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先根据题意得出DB的长,然后证明△BPQ~△BCD,据此利用相似三角形性质分析得出![]() 、
、![]() 、
、![]() ,最后利用角平分线性质进一步求解即可;
,最后利用角平分线性质进一步求解即可;
(2)过点![]() 作
作![]() 于点
于点![]() ,先证明△HMQ~△PQB,由此得出
,先证明△HMQ~△PQB,由此得出![]() ,最后根据三角形面积公式进一步计算即可;
,最后根据三角形面积公式进一步计算即可;
(3)设![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,易得
,易得![]() ,然后进一步证明△DFO~△DCB,由此进一步求解即可.
,然后进一步证明△DFO~△DCB,由此进一步求解即可.
(1)∵四边形![]() 为矩形,
为矩形,
∴![]() 、
、![]() ,∠A=∠C=90°,
,∠A=∠C=90°,
∴![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() 90°,
90°,
∵![]() ,
,
∴△BPQ~△BCD,
∴![]() ,即
,即![]() ,
,
则![]() 、
、![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
故答案为:1;
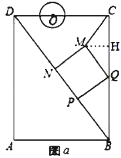
(2)如图![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() 90°,
90°,
则![]() 90°,
90°,
∴![]() ,
,
∴△HMQ~△PQB,
∴![]() ,即
,即![]() ,则
,则![]() ,
,
∴![]() ;
;
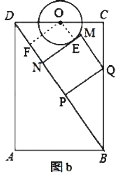
(3)如图![]() ,设
,设![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,
则四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() 90°,
90°,
∵![]() ,
,
∴△DFO~△DCB,
∴![]() ,
,
即![]() ,
,
解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线
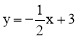 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数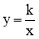 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
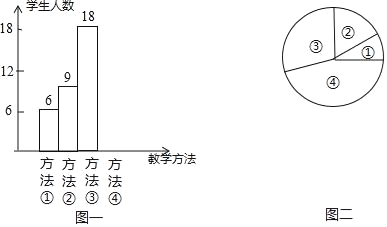
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角
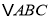 中,
中, ,
,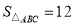 两动点
两动点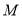 ,
, 分别在
分别在 ,
,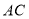 边上滑动且
边上滑动且 ,
,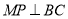 ,
,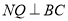 ,得矩形
,得矩形 ,设
,设 的长为
的长为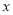 ,矩形
,矩形 的面积为
的面积为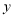 ,则
,则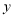 关于
关于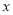 的函数图象大致是( )
的函数图象大致是( )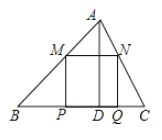
A.
 B.
B.
C.
 D.
D.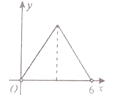
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
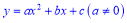 的图象与
的图象与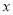 轴交于点
轴交于点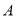 (-1,0),与
(-1,0),与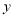 轴的交点在
轴的交点在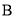 (0,-2)和(0,-1)之间(不包括这两点),对称轴为直线
(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线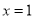 ,下列结论不正确的是( )
,下列结论不正确的是( )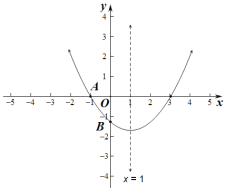
A.
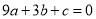 B.
B.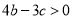 C.
C.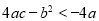 D.
D.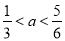
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地,甲乙两车距A地的路程
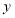 (
(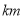 )与乙车行驶时间
)与乙车行驶时间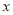 (
(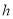 )之间的函数图象如图所示,则下列说法:①
)之间的函数图象如图所示,则下列说法:①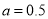 ②甲的速度是60km/h;③乙出发80min追上甲;④乙车在货站装好货准备离开时,甲车距B地150km;⑤当甲乙两车相距30 km时,甲的行驶时间为1 h、3 h、
②甲的速度是60km/h;③乙出发80min追上甲;④乙车在货站装好货准备离开时,甲车距B地150km;⑤当甲乙两车相距30 km时,甲的行驶时间为1 h、3 h、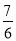 h;其中正确的是__________.
h;其中正确的是__________.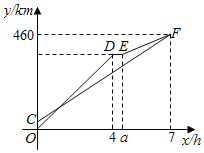
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行抽样调查,从两个城市中所有的饮料自动售卖机中分别抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述数据:对销售金额进行分组,各组的频数如下:
销传金额
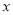
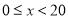
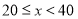
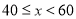
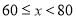
甲
3
6
4
3
乙
2
6
a
b
分析数据:两组样本数据的平均数、中位数如下表所示:
城市
中位数
平均数
众数
甲
C
39.8
45
乙
40
38.9
d
请根据以上信息,回答下列问题:
(1)填空:a=, b=, c=, d=.
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).
相关试题

