【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地,甲乙两车距A地的路程![]() (
(![]() )与乙车行驶时间
)与乙车行驶时间![]() (
(![]() )之间的函数图象如图所示,则下列说法:①
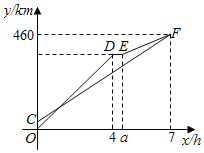
)之间的函数图象如图所示,则下列说法:①![]() ②甲的速度是60km/h;③乙出发80min追上甲;④乙车在货站装好货准备离开时,甲车距B地150km;⑤当甲乙两车相距30 km时,甲的行驶时间为1 h、3 h、
②甲的速度是60km/h;③乙出发80min追上甲;④乙车在货站装好货准备离开时,甲车距B地150km;⑤当甲乙两车相距30 km时,甲的行驶时间为1 h、3 h、![]() h;其中正确的是__________.
h;其中正确的是__________.
参考答案:
【答案】②③
【解析】
根据一次函数的性质和该函数的图象对各项进行求解即可.
∵线段DE代表乙车在途中的货站装货耗时半小时,
∴a=4+0.5=4.5(小时),即①不成立;
∵40分钟=![]() 小时,
小时,
∴甲车的速度为460÷(7+![]() )=60(千米/时),即②成立;
)=60(千米/时),即②成立;
设乙车刚出发时的速度为x千米/时,则装满货后的速度为(x﹣50)千米/时,
根据题意可知:4x+(7﹣4.5)(x﹣50)=460,
解得:x=90.
乙车发车时,甲车行驶的路程为60×![]() =40(千米),
=40(千米),
乙车追上甲车的时间为40÷(90﹣60)=![]() (小时),
(小时),
![]() 小时=80分钟,即③成立;
小时=80分钟,即③成立;
乙车刚到达货站时,甲车行驶的时间为(4+![]() )小时,
)小时,
此时甲车离B地的距离为460﹣60×(4+![]() )=180(千米),
)=180(千米),
即④不成立.
设当甲乙两车相距30 km时,甲的行驶时间为x小时,由题意可得
1)乙车未出发时 ,即![]()
![]()
解得![]()
∵![]()
∴![]() 是方程的解
是方程的解
2)乙车出发时间为![]()
![]()
![]()
![]()
解得![]()
![]()
![]()
![]()
解得![]()
3)乙车出发时间为![]()
![]()
![]()
解得![]()
∵![]()
所以不成立
4)乙车出发时间为![]()
![]()
![]()
![]()
解得![]()
故当甲乙两车相距30 km时,甲的行驶时间为![]() h、1 h、3 h、
h、1 h、3 h、![]() h,故⑤不成立
h,故⑤不成立
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角
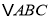 中,
中, ,
,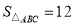 两动点
两动点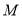 ,
, 分别在
分别在 ,
,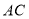 边上滑动且
边上滑动且 ,
,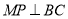 ,
,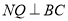 ,得矩形
,得矩形 ,设
,设 的长为
的长为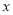 ,矩形
,矩形 的面积为
的面积为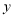 ,则
,则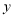 关于
关于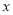 的函数图象大致是( )
的函数图象大致是( )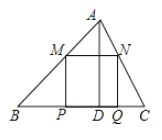
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
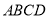 中,
中,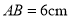 ,
,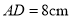 ,点
,点 从点
从点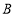 出发,沿对角线
出发,沿对角线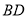 向点
向点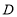 匀速运动,速度为
匀速运动,速度为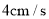 ,过点
,过点 作
作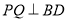 交
交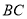 于点
于点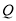 ,以
,以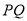 为一边作正方形
为一边作正方形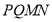 ,使得点
,使得点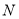 落在射线
落在射线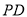 上.点
上.点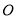 从点
从点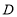 出发,沿
出发,沿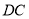 向点
向点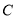 匀速运动,速度为
匀速运动,速度为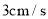 ,以
,以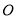 为圆心,
为圆心,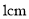 半径作
半径作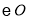 .点
.点 与点
与点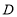 同时出发,设它们的运动时间为
同时出发,设它们的运动时间为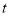 (单位:
(单位: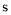 )
)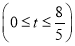 .
.(1)如图1,连接
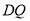 ,若
,若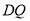 平分
平分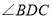 ,则
,则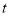 的值为__________
的值为__________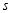 ;
;(2)如图2,连接
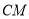 ,设
,设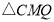 的面积为
的面积为 ,求
,求 关于t的函数关系式;
关于t的函数关系式;(3)在运动过程中,当
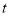 为何值时,
为何值时,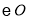 与
与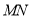 第一次相切?
第一次相切?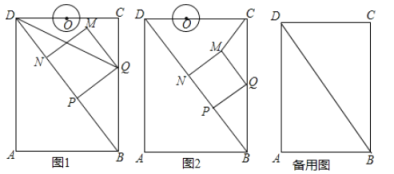
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
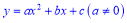 的图象与
的图象与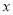 轴交于点
轴交于点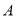 (-1,0),与
(-1,0),与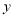 轴的交点在
轴的交点在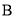 (0,-2)和(0,-1)之间(不包括这两点),对称轴为直线
(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线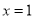 ,下列结论不正确的是( )
,下列结论不正确的是( )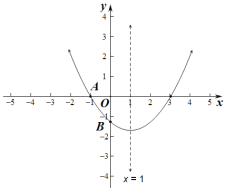
A.
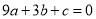 B.
B.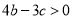 C.
C.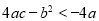 D.
D.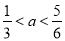
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行抽样调查,从两个城市中所有的饮料自动售卖机中分别抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述数据:对销售金额进行分组,各组的频数如下:
销传金额
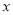
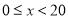
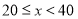
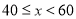
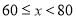
甲
3
6
4
3
乙
2
6
a
b
分析数据:两组样本数据的平均数、中位数如下表所示:
城市
中位数
平均数
众数
甲
C
39.8
45
乙
40
38.9
d
请根据以上信息,回答下列问题:
(1)填空:a=, b=, c=, d=.
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小涛根据学习函数的经验,对函数
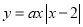 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:(1)下表是
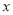 与
与 的几组对应值
的几组对应值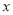
...
-2
-1
0
1
2
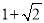
3
...

...
-8
-3
0
m
n
1
3
...
请直接写出:
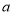 =, m=, n=;
=, m=, n=;(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数
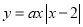 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)(4)请结合画出的函数图象,解决问题:若方程
 有三个不同的解,直接写出
有三个不同的解,直接写出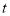 的取值范围.
的取值范围.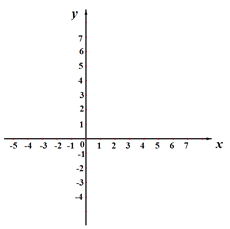
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年,中央全面落实“稳房价”的长效管控机制,重庆房市较上一年大幅降温,11月,LH地产共推出了大平层和小三居两种房型共80套,其中大平层每套面积180平方米,单价1.8万元/平方米,小三居每套面积120平方米,单价1.5万元/平方米.
(1)LH地产11月的销售总额为18720万元,问11月要推出多少套大平层房型?
(2)2019年12月,中央经济会议上重申“房子是拿来住的,不是拿来炒的”,重庆房市成功稳定并略有回落.为年底清盘促销,LH地产调整营销方案,12月推出两种房型的总数量仍为80套,并将大平层的单价在原有基础上每平方米下调
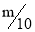 万元(m>0),将小三居的单价在原有基础上每平方米下调
万元(m>0),将小三居的单价在原有基础上每平方米下调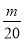 万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
相关试题

