搜索
【题目】如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于82°，则∠OBC=°．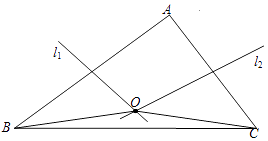 
参考答案：
【答案】8
【解析】解：连接OA，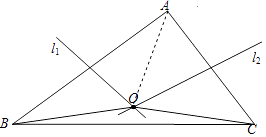 
∵∠BAC=82°，
∴∠ABC+∠ACB=180°﹣82°=98°，
∵AB、AC的垂直平分线交于点O，
∴OB=OA，OC=OA，
∴∠OAB=∠OBA，∠OAC=∠OCA，
∴∠OBC+∠OCB=100°﹣（OBA+∠OCA）=16°，
∴∠OBC=8°，
所以答案是：8．
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．
-
科目： 来源： 题型：
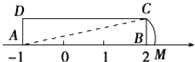
查看答案和解析>>【题目】如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为________________．
【答案】
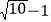
【解析】AC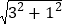＝AM＝
＝
，∴AM＝【题型】填空题
【结束】
11【题目】在△ABC中，AB＝10，AC＝2
，BC边上的高AD＝6，则另一边BC等于_______． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根，比如对于方程
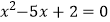，操作步骤是：
第一步：根据方程系数特征，确定一对固定点A（0，1），B（5，2）;
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C 的横坐标m即为该方程的一个实数根（如图1）
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D 的横坐标为n即为该方程的另一个实数根。
（1）在图2 中，按照“第四步“的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）
（2）结合图1，请证明“第三步”操作得到的m就是方程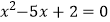 的一个实数根；
（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程
的实数根，请你直接写出一对固定点的坐标；
（4）实际上，（3）中的固定点有无数对，一般地,当
， 
， 
， 
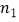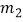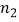与a，b，c之间满足怎样的关系时，点P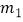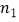（ ， ），Q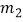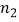（ ， ）就是符合要求的一对固定点？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1= A1A2=1．以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4……依次规律得到等腰直角三角形OA2015A2016，则点A2015的坐标为 __．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A(3，4)，B(1，2)，C(5，1).
(1)如图中作出△ABC关于y轴的对称图形△A1B1C1；
(2)写出点A1，B1，C1的坐标（直接写答案）．
(3)连接OB1，OC1，求△OB1C1的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】=如图，在半径为2的⊙O中，弦AB=2，⊙O上存在点C，使得弦AC=2
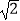，则∠BOC=°．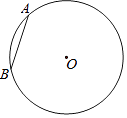 
-
科目： 来源： 题型：
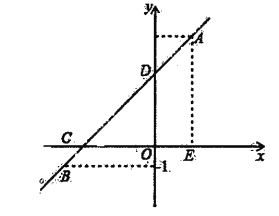
查看答案和解析>>【题目】如图，一次函数的图象l经过点A(2，5)，B（-4，-1）两点.
(1)求一次函数表达式．
(2)若点E在x轴上，且E(2，O)，点C为直线l与x轴的交点，求△CDE的面积.
(3)你能求出点E到直线l的距离吗？
相关试题
