搜索
【题目】如图，在平面直角坐标系中，A(3，4)，B(1，2)，C(5，1).
(1)如图中作出△ABC关于y轴的对称图形△A1B1C1；
(2)写出点A1，B1，C1的坐标（直接写答案）．
(3)连接OB1，OC1，求△OB1C1的面积．
参考答案：
【答案】（1）见解析；（2）A1（-3,4）B1（-1,2）C1（-5,1）；（3）4.5
【解析】
（1）首先确定A、B、C三点关于y轴的对称点，再连接即可；
（2）根据平面直角坐标系写出各点坐标即可；
（3）利用矩形的面积减去周围多余三角形的面积即可．
解：（1）如图所示：△A1B1C1，即为所求；
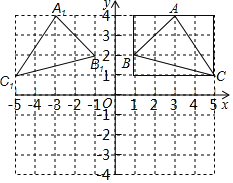
（2）A1（-3，4），B1（-1，2），C1（-5，1）；
故答案为：（-3，4）；（-1，2）；（-5，1）；
（3）OB1，OC1，如图
△OB1C1的面积为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根，比如对于方程
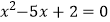，操作步骤是：
第一步：根据方程系数特征，确定一对固定点A（0，1），B（5，2）;
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C 的横坐标m即为该方程的一个实数根（如图1）
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D 的横坐标为n即为该方程的另一个实数根。
（1）在图2 中，按照“第四步“的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）
（2）结合图1，请证明“第三步”操作得到的m就是方程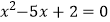 的一个实数根；
（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程
的实数根，请你直接写出一对固定点的坐标；
（4）实际上，（3）中的固定点有无数对，一般地,当
， 
， 
， 
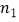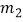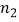与a，b，c之间满足怎样的关系时，点P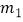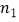（ ， ），Q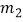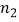（ ， ）就是符合要求的一对固定点？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1= A1A2=1．以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4……依次规律得到等腰直角三角形OA2015A2016，则点A2015的坐标为 __．
-
科目： 来源： 题型：
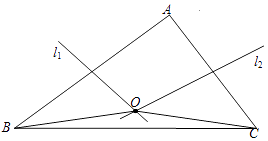
查看答案和解析>>【题目】如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于82°，则∠OBC=°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】=如图，在半径为2的⊙O中，弦AB=2，⊙O上存在点C，使得弦AC=2
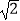，则∠BOC=°． 
-
科目： 来源： 题型：
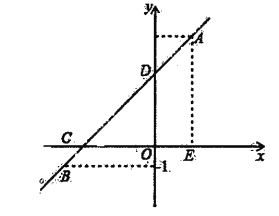
查看答案和解析>>【题目】如图，一次函数的图象l经过点A(2，5)，B（-4，-1）两点.
(1)求一次函数表达式．
(2)若点E在x轴上，且E(2，O)，点C为直线l与x轴的交点，求△CDE的面积.
(3)你能求出点E到直线l的距离吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读：已知a+b＝﹣4，ab＝3，求a2+b2的值．
解：∵a+b＝﹣4，ab＝3，
∴a2+b2＝(a+b)2﹣2ab＝(﹣4)2﹣2×3＝10．
请你根据上述解题思路解答下面问题：
(1)已知a﹣b＝﹣3，ab＝﹣2，求(a+b)(a2﹣b2)的值．
(2)已知a﹣c﹣b＝﹣10，(a﹣b)c＝﹣12，求(a﹣b)2+c2的值．
相关试题
