【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。

(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
参考答案:
【答案】
(1)
解:如图2所示:
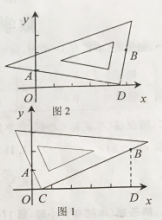
(2)
证明:在图1中,过点B作BD⊥x轴,交x轴于点D.
根据题意可证△AOC∽△CDB.
∴![]() .
.
∴![]() .
.
∴m(5-m)=2.
∴m2-5m+2=0.
∴m是方程x2-5x+2=0的实数根.
(3)
解:方程ax2+bx+c=0(a≠0)可化为
x2+![]() x+
x+![]() =0.
=0.
模仿研究小组作法可得:A(0,1),B(-![]() ,
,![]() )或A(0,
)或A(0,![]() ),B(-
),B(-![]() ,c)等.
,c)等.
(4)
解:以图3为例:P(m1,n1)Q(m2,n2),
设方程的根为x,根据三角形相似可得.![]() =
=![]() .
.
上式可化为x2-(m1+m2)x+m1m2+n1n2=0.
又ax2+bx+c=0,
即x2+![]() x+
x+![]() =0.
=0.
比较系数可得:m1+m2=-![]() .
.
m1m2+n1n2=![]() .
.

【解析】(1)根据题目中给的操作步骤操作即可得出图2中的图.
(2)在图1中,过点B作BD⊥x轴,交x轴于点D.依题意可证△AOC∽△CDB.然后根据相似三角形对应边的比相等列出式子,化简后为m2-5m+2=0,从而得证。
(3)将方程ax2+bx+c=0(a≠0)可化为x2+![]() x+
x+![]() =0.模仿研究小组作法即可得答案。
=0.模仿研究小组作法即可得答案。
(4)以图3为例:P(m1,n1)Q(m2,n2),设方程的根为x,根据三角形相似可得.![]() =
=![]() .化简后为x2-(m1+m2)x+m1m2+n1n2=0.
.化简后为x2-(m1+m2)x+m1m2+n1n2=0.
又x2+![]() x+
x+![]() =0.再依据相对应的系数相等即可求出。
=0.再依据相对应的系数相等即可求出。
【考点精析】利用根与系数的关系和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球
总次数
40
80
120
160
200
240
280
320
360
400
摸到黄球的次数
14
23
38
52
67
86
97
111
120
136
摸到黄球的频率
35%
32%
33%
35%
35%
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ②
②  ③
③ 
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当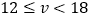 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值 -
科目: 来源: 题型:
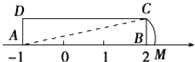
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
【答案】
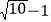
【解析】AC=AM=
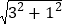 =
= ,∴AM=
,∴AM=
【题型】填空题
【结束】
11【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1= A1A2=1.以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4……依次规律得到等腰直角三角形OA2015A2016,则点A2015的坐标为 __.

-
科目: 来源: 题型:
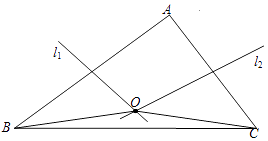
查看答案和解析>>【题目】如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(3,4),B(1,2),C(5,1).
(1)如图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1,B1,C1的坐标(直接写答案).
(3)连接OB1,OC1,求△OB1C1的面积.

相关试题

