【题目】如图,抛物线y= ![]() (x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
参考答案:
【答案】
(1)
解:顶点D的坐标为(3,﹣1).
令y=0,得 ![]() (x﹣3)2﹣1=0,
(x﹣3)2﹣1=0,
解得:x1=3+ ![]() ,x2=3﹣
,x2=3﹣ ![]() ,
,
∵点A在点B的左侧,
∴A(3﹣ ![]() ,0),B(3+
,0),B(3+ ![]() ,0)
,0)
(2)
方法一:
证明:如答图1,过顶点D作DG⊥y轴于点G,则G(0,﹣1),GD=3.

令x=0,得y= ![]() ,
,
∴C(0, ![]() ).
).
∴CG=OC+OG= ![]() +1=
+1= ![]() ,
,
∴tan∠DCG= ![]() .
.
设对称轴交x轴于点M,则OM=3,DM=1,AM=3﹣(3﹣ ![]() )=
)= ![]() .
.
由OE⊥CD,易知∠EOM=∠DCG.
∴tan∠EOM=tan∠DCG= ![]() =
= ![]() ,
,
解得EM=2,
∴DE=EM+DM=3.
在Rt△AEM中,AM= ![]() ,EM=2,由勾股定理得:AE=
,EM=2,由勾股定理得:AE= ![]() ;
;
在Rt△ADM中,AM= ![]() ,DM=1,由勾股定理得:AD=
,DM=1,由勾股定理得:AD= ![]() .
.
∵AE2+AD2=6+3=9=DE2,
∴△ADE为直角三角形,∠EAD=90°.
设AE交CD于点F,
∵∠AEO+∠EFH=90°,∠ADC+AFD=90°,∠EFH=∠AFD(对顶角相等),
∴∠AEO=∠ADC
方法二:
∵C(0, ![]() ),D(3,﹣1),
),D(3,﹣1),
∴KCD= ![]() ,
,
∵OE⊥CD,∴KCD×KOE=﹣1,
∴KOE= ![]() ,
,
∴lOE:y= ![]() x,把x=3代入,得y=2,
x,把x=3代入,得y=2,
∴E(3,2),
∵A(3﹣ ![]() ,0),D(3,﹣1),
,0),D(3,﹣1),
∴KEA= ![]() =
= ![]() ,
,
∵KAD= ![]() ,
,
∴KEA×KAD=﹣1,
∴EA⊥AD,∠EHD=∠EAD,
∵∠EFH=∠AFD,
∴∠AEO=∠ADC
(3)
方法一:
解:依题意画出图形,如答图2所示:

由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2﹣1,
要使切线长PQ最小,只需EP长最小,即EP2最小.
设点P坐标为(x,y),由勾股定理得:EP2=(x﹣3)2+(y﹣2)2.
∵y= ![]() (x﹣3)2﹣1,
(x﹣3)2﹣1,
∴(x﹣3)2=2y+2.
∴EP2=2y+2+(y﹣2)2=(y﹣1)2+5
当y=1时,EP2有最小值,最小值为5.
将y=1代入y= ![]() (x﹣3)2﹣1,得
(x﹣3)2﹣1,得 ![]() (x﹣3)2﹣1=1,
(x﹣3)2﹣1=1,
解得:x1=1,x2=5.
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去.
∴P(5,1).
∵△EQ2P为直角三角形,
∴过点Q2作x轴的平行线,再分别过点E,P向其作垂线,垂足分别为M点和N点.
由切割线定理得到Q2P=Q1P=2,EQ2=1
设点Q2的坐标为(m,n)
则在Rt△MQ2E和Rt△Q2NP中建立勾股方程,即(m﹣3)2+(n﹣2)2=1①,(5﹣m)2+(n﹣1)2=4②
①﹣②得n=2m﹣5③
将③代入到①得到
m1=3(舍,为Q1)
m2= ![]()
再将m= ![]() 代入③得n=
代入③得n= ![]() ,
,
∴Q2( ![]() ,
, ![]() )
)
此时点Q坐标为(3,1)或( ![]() ,
, ![]() )
)
方法二:由⊙E的半径为1,得PQ2=EP2﹣1,要使切线长PQ最小,只需EP长最小,即EP2最小,
设点P坐标为(x,y),EP2=(x﹣3)2+(y﹣2)2,
∵y= ![]() (x﹣3)2﹣1,∴(x﹣3)2=2y+2,
(x﹣3)2﹣1,∴(x﹣3)2=2y+2,
∴EP2=2y+2+(y﹣2)2=(y﹣1)2+5,
∴当y=1时,EP2有最小值,将y=1代入y= ![]() (x﹣3)2﹣1得:x1=1,x2=5,
(x﹣3)2﹣1得:x1=1,x2=5,
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去,∴P(5,1),
显然Q1(3,1),
∵Q1Q2被EP垂直平分,垂足为H,
∴KQ1Q2×KEP=﹣1,
∴KEP= ![]() =﹣
=﹣ ![]() ,KQ1Q2=2,
,KQ1Q2=2,
∵Q1(3,1),
∴lQ1Q2:y=2x﹣5,
∵lEP:y=﹣ ![]() x+
x+ ![]() ,
,
∴x= ![]() ,y=
,y= ![]() ,
,
∴H( ![]() ,
, ![]() ),
),
∵H为Q1Q2的中点,
∴Hx= ![]() ,
,
HY= ![]() ,
,
∴Q2(x)=2× ![]() ﹣3=
﹣3= ![]() ,
,
Q2(Y)=2× ![]() ﹣1=
﹣1= ![]() ,
,
∴Q2( ![]() ,
, ![]() ).
).

【解析】(1)根据二次函数性质,求出点A、B、D的坐标;(2)如何证明∠AEO=∠ADC?如答图1所示,我们观察到在△EFH与△ADF中:∠EHF=90°,有一对对顶角相等;因此只需证明∠EAD=90°即可,即△ADE为直角三角形,由此我们联想到勾股定理的逆定理.分别求出△ADE三边的长度,再利用勾股定理的逆定理证明它是直角三角形,由此问题解决;(3)依题意画出图形,如答图2所示.由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2﹣1,要使切线长PQ最小,只需EP长最小,即EP2最小.利用二次函数性质求出EP2最小时点P的坐标,并进而求出点Q的坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.

(1)当t= 秒时,则OP= , S△ABP=;
秒时,则OP= , S△ABP=;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQBP=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) (2
 -3
-3 )÷
)÷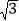 ; (2) (
; (2) ( -
-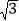 )2+2
)2+2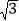 ×
× ;
;(3)
 ; (4) (
; (4) ( -2
-2 )×
)×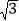 -4
-4 ;
;(5)(
 -1)(
-1)( +1)-(-
+1)-(- )-2+|1-
)-2+|1- |-(π-2)0+
|-(π-2)0+ ;
;(6)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形OABC的顶点O在原点。
(1)如图①,点C的坐标为(
 ,
, ),且实数
),且实数 ,
, 满足
满足 ,求C点的坐标及线段0C的长度;
,求C点的坐标及线段0C的长度;(2)如图②,点F在BC上,AB交x轴于点E,EF,OC的延长线交于点G,EG=OG,求∠EOF的度数;
(3)如图③,将(1)中正方形OABC绕点O顺时针旋转,使OA落在y轴上,E为AB上任意一点,OE的垂直平分线交x轴于点G,交OE于点P,连接EG交BC于点F,求△BEF的周长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
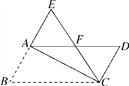
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x=
 -1,求x2+3x-1的值;
-1,求x2+3x-1的值;(2)若|x-4|+
 +(z+27)2=0,求
+(z+27)2=0,求 +
+ -
- 的值;
的值;(3)已知
 ,求
,求 的值.
的值.
相关试题

