【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB+AP=PD,继而可得方程6+t=(8-t),解此方程即可求得答案
本题解析:.
解:(1)∵四边形ABCD是矩形,∴AD∥BC,
∴∠PDO=∠QBO,∵O为BD的中点,∴DO=BO,
在△PDO和△QBO中,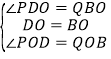
∴△PDO≌△QBO(ASA),∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,∴PD=8﹣t,
(3)∵PB=PD,∴PB2=PD2,即AB2+AP2=PD2,
∴62+t2=(8-t)2,解得 t=![]() ,
,
∴当t=![]() 时,PB=PD.
时,PB=PD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解初二年级480名学生到校上学的方式,在初二随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).


⑴问:在这次调查中,一共抽取了多少名学生?
⑵补全条形统计图;
⑶估计该校初二年级学生中有多少人乘坐公交车上学.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5
 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为: (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为: (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.(1)填空:
 记为( , ),
记为( , ), 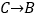 记为( , );
记为( , );(2)若甲虫的行走路线为:
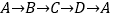 ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:
(1)(-3
 )+(+8
)+(+8 )-(-5
)-(-5 );
);(2)(-
 )+(+
)+(+ )+(+
)+(+ )+(-1
)+(-1 );
);(3)(-3
 )-(-
)-(- )+(-0.5)+3
)+(-0.5)+3 ;
;(4)(+3
 )+(-2
)+(-2 )-(-5
)-(-5 )-(+
)-(+ );
);(5)(-0.25)+(-3)-|-1
 |-(-3);
|-(-3);(6)(+
 )+(+17)+(-1
)+(+17)+(-1 )-(+7)-(-2
)-(+7)-(-2 )+(-
)+(- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别
从A、C两点同时以1cm/s的相同的速度向C、A运动.

(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,
四边形DEBF为矩形.
相关试题

