【题目】在平面直角坐标系中,正方形OABC的顶点O在原点。
(1)如图①,点C的坐标为(![]() ,
,![]() ),且实数
),且实数![]() ,
,![]() 满足
满足![]() ,求C点的坐标及线段0C的长度;
,求C点的坐标及线段0C的长度;
(2)如图②,点F在BC上,AB交x轴于点E,EF,OC的延长线交于点G,EG=OG,求∠EOF的度数;
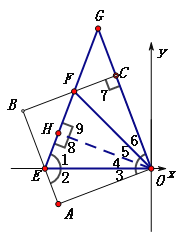
(3)如图③,将(1)中正方形OABC绕点O顺时针旋转,使OA落在y轴上,E为AB上任意一点,OE的垂直平分线交x轴于点G,交OE于点P,连接EG交BC于点F,求△BEF的周长。

参考答案:
【答案】(1)![]() (2)45°(3)2
(2)45°(3)2![]()
【解析】分析:(1)根据非负数的性质和二次根式有意义的条件可得b=3,a=-1,即可的点C的坐标,再由勾股定理求得OC的长;(2)过点O作OH⊥EF于H,证明△OEA≌△OEH和 Rt△OHF≌Rt△OCF,根据全等三角形的性质可得∠3=∠4,∠5=∠6,又因∠3+∠4+∠5+∠6=∠AOC=90°,即可求得∠EOF=45°;(3)过点O作OH⊥EF于H,连OF,证明△OEA≌△OEH和Rt△OHF≌Rt△OCF,根据全等三角形的性质可得AE=EH,OH=OA,HF=FC,即可得△BEF的周长=BE+EH+HF+BF=BE+AE+CF+BF=AB+BC=2![]() .
.
详解:
(1)∵b-3≥0,3-b≥0,
∴b=3,a=-1,
∴C(-1,3).
过C作CD垂直y轴于点D,则OD=3,DC=1,
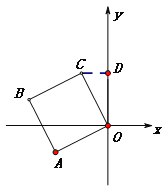
∴OC=![]() ;
;
(2)过点O作OH⊥EF于H,
∵四边形OABC是正方形,
∴OA=OC,∠A=∠7=∠AOC=90°,AB∥CO,
∴∠2=∠COE又EG=OG,
∴∠1=∠COE,
∴∠1=∠2,
又OH⊥EF,
∴∠9=∠8=∠A=90°,
∴在△OEA和△OEH中,
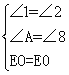 ,
,
∴△OEA≌△OEH(AAS),
∴∠3=∠4,OH=OA;
又OA=OC,
∴OH=OC,
又∠9=∠7=90°,
∴在Rt△OHF和Rt△OCF中,
![]() ,
,
∴Rt△OHF≌Rt△OCF(HL),
∴∠5=∠6,
又∠3+∠4+∠5+∠6=∠AOC=90°,
∴2∠4+2∠5=90°,
即∠4+∠5=45°,
即∠EOF=45°;
(3)过点O作OH⊥EF于H,连OF,
∵四边形OABC是正方形,
∴OA=OC,∠10=∠7=∠AOC=90°,AB∥CO,
∴∠2=∠COE又PG垂直平分OE,
∴EG=OG,
∴∠1=∠COE,
∴∠1=∠2 ,
又OH⊥EF,
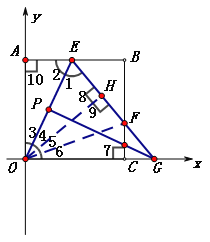
∴∠9=∠8=∠10=90°,
∴在△OEA和△OEH中,

∴△OEA≌△OEH(AAS);
∴AE=EH,OH=OA,
又OA=OC,
∴OH=OC,
又∠9=∠7=90°,
∴在Rt△OHF和Rt△OCF中,
![]() ,
,
∴Rt△OHF≌Rt△OCF(HL);
∴HF=FC,
∴△BEF的周长=BE+EH+HF+BF
=BE+AE+CF+BF
=AB+BC
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) (2
 -3
-3 )÷
)÷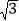 ; (2) (
; (2) ( -
-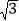 )2+2
)2+2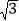 ×
× ;
;(3)
 ; (4) (
; (4) ( -2
-2 )×
)×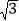 -4
-4 ;
;(5)(
 -1)(
-1)( +1)-(-
+1)-(- )-2+|1-
)-2+|1- |-(π-2)0+
|-(π-2)0+ ;
;(6)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 (x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
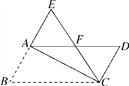
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x=
 -1,求x2+3x-1的值;
-1,求x2+3x-1的值;(2)若|x-4|+
 +(z+27)2=0,求
+(z+27)2=0,求 +
+ -
- 的值;
的值;(3)已知
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,点A(-1,2),B(-3,-2),C(3,-3)
①在直角坐标系中,画出△ABC,并求△ABC的面积;
②在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.

相关试题

