【题目】如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

参考答案:
【答案】(1)ON⊥CD,理由见解析;(2)157.5°
【解析】
(1)根据垂直的定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,再利用等量代换可得∠2+∠AOC=90°,从而可得ON⊥CD.
(2)由题意可得∠1=![]() ∠BOC=
∠BOC=![]() (∠1+90°) ,进而可得∠MOD=90°+∠BOD=90°+∠AOC=180°-∠1,再代入∠1的度数即可的解.
(∠1+90°) ,进而可得∠MOD=90°+∠BOD=90°+∠AOC=180°-∠1,再代入∠1的度数即可的解.
(1)ON⊥CD.理由如下:
∵OM⊥AB,∴∠AOM=90°,
∴∠1+∠AOC=90°,
又∵∠1=∠2,∴∠2+∠AOC=90°,
即∠CON=90°,∴ON⊥CD.
(2) ∠1=![]() ∠BOC=
∠BOC=![]() (∠1+90°) ,
(∠1+90°) ,
∵∠1=22.5°,∴ ∠MOD=90°+∠BOD=90°+∠AOC=180°-∠1= 157.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
电视机
电饭煲
甲商店/元
100
60
乙商店/元
80
50
(1)设集团调配给甲商店x台电视机,则调配给甲商店电饭煲 台,调配给乙商店电视机 台、电饭煲 台;
(2)求出x的取值范围;
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A,B两点,分别对应的数为a,b。| a |=3,| b |=9,

(1)求a与b的值。
(2)求出线段AB的长度。
(3)若数轴上有一点C,且C到B的距离是C到A距离的3倍,直接写出点C所表示的数。
(4)点P从点A出发,先向左移动1个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度········,求出1889次移动后的点P所表示的数
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E、F分别在CD、BC边上,
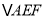 是等边三角形.以下结论:①
是等边三角形.以下结论:①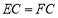 ;②
;②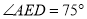 ;③
;③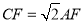 ;④EF的垂直平分线是直线AC.正确结论个数有( )个.
;④EF的垂直平分线是直线AC.正确结论个数有( )个.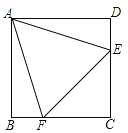
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一次函数的图象经过
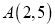 ,
,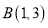 两点.求这个一次函数的解析式;并判断点
两点.求这个一次函数的解析式;并判断点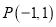 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;(2)如图所示,点D是等边
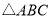 内一点,
内一点,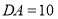 ,
,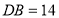 ,
,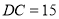 ,将
,将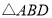 绕点A逆时针旋转到
绕点A逆时针旋转到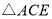 的位置,求
的位置,求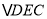 的周长.
的周长.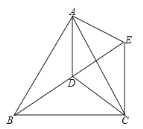
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=
 于点C、D.
于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>
 的解集.
的解集.
-
科目: 来源: 题型:
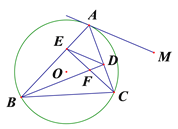
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,CE⊥AB于点E,BD⊥AC于点D,BD、CE相交于点F,连结ED.
(1)若∠ABC=45°,证明AE=EF;
(2)求证:△AED∽△ACB;
(3)过点A的直线AM∥ED, AM是⊙O的切线吗?说明理由.
相关试题

