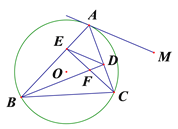
【题目】如图,△ABC是⊙O的内接三角形,CE⊥AB于点E,BD⊥AC于点D,BD、CE相交于点F,连结ED.
(1)若∠ABC=45°,证明AE=EF;
(2)求证:△AED∽△ACB;
(3)过点A的直线AM∥ED, AM是⊙O的切线吗?说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)是,证明见解析.
【解析】试题分析:(1)由ASA证明△BEF≌△CEA即可;
(2)先证明△AEC∽△ADB,得到AE:AD=AC:AB,再证明△AED∽△ACB即可;
(3)连接AO并延长交⊙O于N,连接NC.由△AED∽△ACB,得到∠ADE=∠ABC,由同弧所对的圆周角相等,得到∠ABC=∠N,等量代换得到∠ADE=∠N.由平行线的性质得到∠MAC=∠ADE,从而∠MAC=∠N.由AN为直径,得到∠CAN+∠N=90°,进而∠CAN+∠MAC=90°,即可得到结论.
试题解析:解:(1)∵∠ABC=45°,CE⊥AB,即∠BEC=90°,∴∠ECB=45°=∠EBC,∴EB=EC.
∵CE⊥AB,BD⊥AC,∴∠BEC=∠BDC=90°,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°.
∵∠EFB=∠DFC,∴∠EBF=∠DCF.
在△BEF和△CEA中,∵∠FBE=∠ACE,BE=CE,∠BEF=∠CEA=90°,∴△BEF≌△CEA,∴AE=EF.
(2)∵∠EBF=∠DCF,∠A=∠A,∴△AEC∽△ADB,∴AE:AD=AC:AB.∵∠A=∠A,∴△AED∽△ACB;
(3)AM是⊙O的切线.理由如下:
连接AO并延长交⊙O于N,连接NC.∵△AED∽△ACB,∴∠ADE=∠ABC.∵∠ABC=∠N,∴∠ADE=∠N.∵AM∥ED,∴∠MAC=∠ADE,∴∠MAC=∠N.∵AN为直径,∴∠NCA=90°,∴∠CAN+∠N=90°,∴∠CAN+∠MAC=90°,∴∠MAO=90°,∴AM是⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1=
 ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一次函数的图象经过
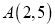 ,
,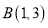 两点.求这个一次函数的解析式;并判断点
两点.求这个一次函数的解析式;并判断点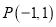 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;(2)如图所示,点D是等边
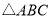 内一点,
内一点,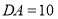 ,
,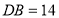 ,
,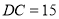 ,将
,将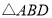 绕点A逆时针旋转到
绕点A逆时针旋转到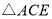 的位置,求
的位置,求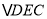 的周长.
的周长.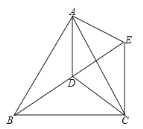
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=
 于点C、D.
于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
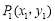 ,
,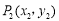 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把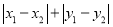 叫做
叫做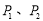 两点间的“直角距离”,记作
两点间的“直角距离”,记作 .
.(1)令
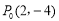 ,
,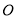 为坐标原点,则
为坐标原点,则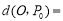 ________;
________; (2)已知
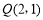 ,动点
,动点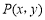 满足
满足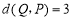 ,且
,且 均为整数:
均为整数:①满足条件的点
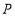 有多少个?
有多少个?②若点
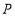 在直线
在直线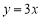 上,请写出符合条件的点
上,请写出符合条件的点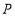 的坐标.
的坐标.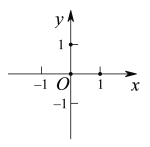
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,百位数是
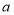 ,十位数是
,十位数是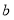 ,个位数是
,个位数是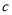 ,我们可以记作
,我们可以记作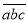 ,
, 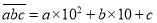 表示,例如
表示,例如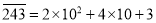 ,仿照上面的例子,
,仿照上面的例子,(1)
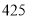 可以用 表示;
可以用 表示;(2)
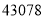 可以用 表示;
可以用 表示;(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给
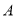 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由.
相关试题

