【题目】如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).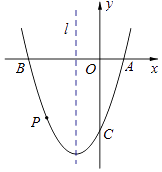
(1)直接写出抛物线的解析式;
(2)小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵A(1,0),对称轴l为x=﹣1,
∴B(﹣3,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=x2+2x﹣3;
(2)
解:如图1,过点P作PM⊥x轴于点M,
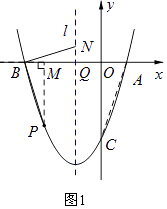
设抛物线对称轴l交x轴于点Q.
∵PB⊥NB,∴∠PBN=90°,
∴∠PBM+∠NBQ=90°.
∵∠PMB=90°,
∴∠PBM+∠BPM=90°.
∴∠BPM=∠NBQ.
又∵∠BMP=∠BNQ=90°,PB=NB,
∴△BPM≌△NBQ.
∴PM=BQ.
∵抛物线y=x2+2x﹣3与x轴交于点A(1,0)和点B,且对称轴为x=﹣1,
∴点B的坐标为(﹣3,0),点Q的坐标为(﹣1,0).∴BQ=2.∴PM=BQ=2.
∵点P是抛物线y=x2+2x﹣3上B、C之间的一个动点,
∴结合图象可知点P的纵坐标为﹣2,
将y=﹣2代入y=x2+2x﹣3,得﹣2=x2+2x﹣3,
解得x1=﹣1﹣ ![]() ,x2=﹣1+
,x2=﹣1+ ![]() (舍去),
(舍去),
∴此时点P的坐标为(﹣1﹣ ![]() ,﹣2)
,﹣2)
(3)
解:存在.
如图2,连接AC.
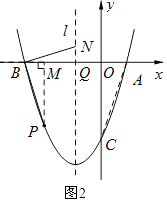
可设点P的坐标为(x,y)(﹣3<x<0),则y=x2+2x﹣3,
∵点A(1,0),∴OA=1.
∵点C是抛物线与y轴的交点,
∴令x=0,得y=﹣3.即点C(0,﹣3).
∴OC=3.
由(2)可知S四边形PBAC=S△BPM+S四边形PMOC+S△AOC
= ![]() BMPM+
BMPM+ ![]() (PM+OC)OM+
(PM+OC)OM+ ![]() OAOC
OAOC
= ![]() (x+3)(﹣y)+
(x+3)(﹣y)+ ![]() (﹣y+3)(﹣x)+
(﹣y+3)(﹣x)+ ![]() ×1×3
×1×3
=﹣ ![]() y﹣
y﹣ ![]() x+
x+ ![]() .
.
将y=x2+2x﹣3代入可得S四边形PBAC=﹣ ![]() (x2+2x﹣3)﹣
(x2+2x﹣3)﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() .
.
∵﹣ ![]() <0,﹣3<x<0,
<0,﹣3<x<0,
∴当x=﹣ ![]() 时,S四边形PBAC有最大值
时,S四边形PBAC有最大值 ![]() .此时,y=x2+2x﹣3=﹣
.此时,y=x2+2x﹣3=﹣ ![]() .
.
∴当点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )时,四边形PBAC的面积最大,最大值为
)时,四边形PBAC的面积最大,最大值为 ![]() .
.
【解析】(1)由对称轴可求得B点坐标,结合A、B两点坐标,利用待定系数法可求得抛物线解析式;(2)过点P作PM⊥x轴于点M,设抛物线对称轴l交x轴于点Q.可证明△BPM≌△NBQ,则可求得PM=BQ,可求得P点的纵坐标,利用抛物线解析式可求得P点坐标;(3)连接AC,设出P点坐标,则可表示出四边形PBAC的面积,再利用二次函数的性质可求得其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求
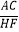 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 的值为 .
的值为 . 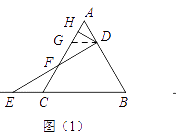
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是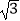 :1,求
:1,求  的值.
的值.
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记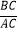 =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 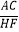 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(a+b)2﹣b(2a+b)
(2)解不等式:(3x+4)(3x-4)<9(x-2)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
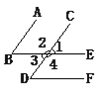
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读材料,再尝试解决问题:
完全平方式
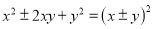 以及
以及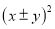 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求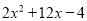 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:解:原式 =
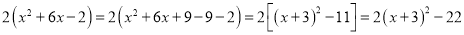 .
.因为无论
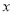 取什么数,都有
取什么数,都有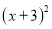 的值为非负数,所以
的值为非负数,所以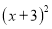 的最小值为0;此时
的最小值为0;此时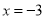 时,进而
时,进而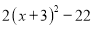 的最小值是
的最小值是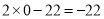 ;所以当
;所以当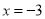 时,原多项式的最小值是
时,原多项式的最小值是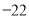 .
.请根据上面的解题思路,探求:
⑴.多项式
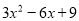 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的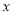 的取值;
的取值;⑵.多项式
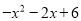 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的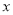 的取值.
的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若
 是
是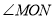 的平分线
的平分线 上一点,点
上一点,点 在
在 上,此时,在
上,此时,在 截取
截取 ,连接
,连接 ,根据三角形全等的判定
,根据三角形全等的判定 ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿ 和⊿
和⊿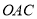 ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:
如图2,在非等边⊿
 中,
中,  ,
,  分别是
分别是 的平分线,且
的平分线,且 交于点
交于点 .求证:
.求证:  .
.
相关试题

