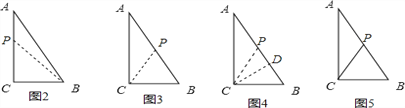
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

参考答案:
【答案】(1)△ABP的周长为7+![]() ;
;
(2)当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形.
【解析】试题分析:(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长.
(2)因为AB与CB,由勾股定理得AC=4cm,因为AB为5cm,所以必须使AC=CB,或CB=AB,所以必须使AC或AB等于3,有两种情况,△BCP为等腰三角形.
试题解析:(1)如图1,由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2,
∵∠C=90°,
∴PB=![]()
∴△ABP的周长为:AP+PB+AB=2+5+![]() =7+
=7+![]()
(2)①如图2,若P在边AC上时,BC=CP=3cm,
此时用的时间为3s,△BCP为等腰三角形;
②若P在AB边上时,有三种情况:
i)如图3,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,
所以用的时间为6s,△BCP为等腰三角形;
ii)如图4,若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm,
作CD⊥AB于点D,
在Rt△PCD中,PD=1.8,
所以BP=2PD=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形;
ⅲ)如图5,若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠B=32°,∠C =48°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F,求∠ADF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:4x4x2﹣(﹣2x2)3﹣3x8÷x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于
 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.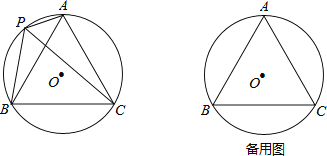
-
科目: 来源: 题型:
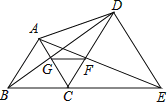
查看答案和解析>>【题目】如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
(1)△ACE≌△BCD; (2)
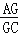 =
=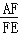 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m+1)x2+2mx﹣3=0是一元二次方程,则m的取值是( )
A.任意实数B.m≠1C.m≠﹣1D.m>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=-2x向下平移两个单位,所得的直线是( )
A. y=-2x-2 B. y=-2x+2
C. y=-2(x-2) D. y=-2(x+2)
相关试题

