【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

参考答案:
【答案】(1)答案见解析;(2)证明见解析
【解析】
(1)根据题意画出图形,证明两个三角形不全等即可;
(2)作GB⊥CA交CA的延长线于G,作DH⊥FE交FE的延长线于H,分别证明△ABG≌△EDH,Rt△CBG≌Rt△FDH,根据全等三角形的性质得到∠C=∠F,利用AAS定理证明即可.
(1)如图1,
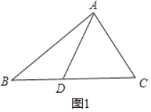
在△ABD和△ABC中,
AB=AB,∠B=∠B,AD=AC,
△ABD和△ABC不全等;
(2)如图2,
作GB⊥CA交CA的延长线于G,作DH⊥FE交FE的延长线于H,
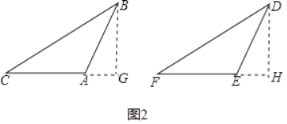
在△ABG和△EDH中,
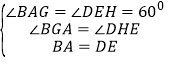 ,
,
∴△ABG≌△EDH(AAS)
∴BG=DH,
在Rt△CBG和Rt△FDH中,
![]() ,
,
∴Rt△CBG≌Rt△FDH(HL)
∴∠C=∠F,
在△ABC和△EDF中,
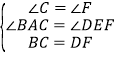 ,
,
∴△ABC≌△EDF(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球不放回,再随机地摸出一个小球,则两次摸出的小球的标号的和为奇数的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,﹣4),B(5,﹣4),C(4,﹣1)
(1)求出△ABC的面积;
(2)若把△ABC向上平移2个单位长度,再向左平移4个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写出B′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为10cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以1cm/s的速度同时开始运动,运动过程中DE与BC相交于点P,点D运动到点A后两点同时停止运动.
(1)当△ADE是直角三角形时,求D,E两点运动的时间;
(2)求证:在运动过程中,点P始终是线段DE的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条高AD,BE交于点F,∠ABC=45°,∠BAC=60°.
(1)求证:DF=DC;
(2)连接CF,求证:AB=AC+CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
小聪在解方程组
 时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:
时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:解:将方程②变形为:

即

把方程①代入方程③得:
 解得
解得
把
 代入方程①得
代入方程①得
∴方程组的解是

(1)模仿小聪的解法,解方程组

(2)已知x,y满足方程组
 ,解答:
,解答:(ⅰ)求
 的值;
的值; (ⅱ)求
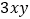 的值.
的值.
相关试题

