搜索
【题目】如图，海中有一个小岛A，它的周围15海里内有暗礁，今有货船由西向东航行，开始在A岛南偏西60° 的B处，往东航行20海里后到达该岛南偏西30° 的C处后，货船继续向东航行，你认为货船航行途中_____ 触礁的危险．（填写：“有”或“没有”）
参考数据：sin60°=cos30°≈0.866．
参考答案：
【答案】没有．
【解析】
货轮在B处时位于A岛的南偏西60°，在C处时位于南偏西30°，所以∠BAC=30°，又因为∠ABC=30°，所以BC=AC=20，根据题意可求出A到BC的最短距离，和15比较可得答案．
∵∠BAD=60°，∠CAD=30°，∴∠BAC=30°．
又∵∠ABC=30°，∴AC=BC=20，∴CD=
AC=×20=10，AD=
=10
＞15，因为A岛到货轮的航线的最短距离大于15，所以没有危险．
故答案为：没有．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，
、
、
三边的长分别为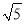
、
、
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图①所示．这样不需求的高，而借用网格就能计算出它的面积．（1）请你将
的面积直接填写在横线上．__________________（2）我们把上述求
面积的方法叫做构图法．若三边的长分别为
、
、
（
），请利用图②的正方形网格（每个小正方形的边长为
）画出相应的，并求出它的面积．（3） 若△ABC三边的长分别为
、
、
(m＞0，n＞0，且m≠n)，请利用图③的长方形网格试运用构图法求出这三角形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
的图象与x轴、y轴分别交于A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC=30°。（1）求AC的长度；
（2）如果在第二象限内有一点
，试求四边形AOPB的面积S与m之间的函数关系式，并求当△APB与△ABC面积相等时m的值。（3）是否存在使△QAB是等腰三角形并且在坐标轴上的点Q？若存在，请写出点Q所有可能的坐标；若不存在，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=
﹣x﹣3．（1）用配方法求函数图象顶点坐标、对称轴，并写出图象的开口方向；
（2）在所给网格中建立平面直角坐标系井直接画出此函数的图象．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图， 直线
与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点， 点P为OA上一动点， 当PC+PD最小时， 点P的坐标为（ ）
A.（-4，0）B.（-1，0）C.(-2,0)D.(-3,0)
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB=90°，AC=40m，BC=30m．线段CD是一条水渠，且D点在边AB上，已知水渠的造价为800元
，问：当水渠的造价最低时，CD长为多少米？最低造价是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明和小亮计划暑期结伴参加志愿者活动．小明想参加敬老服务活动，小亮想参加文明礼仪宣传活动．他们想通过做游戏来决定参加哪个活动，于是小明设计了一个游戏，游戏规则是：在三张完全相同的卡片上分别标记4、5、6三个数字，一人先从三张卡片中随机抽出一张，记下数字后放回，另一人再从中随机抽出一张，记下数字，若抽出的两张卡片标记的数字之和为偶数，则按照小明的想法参加敬老服务活动，若抽出的两张卡片标记的数字之和为奇数，则按照小亮的想法参加文明礼仪宣传活动．你认为这个游戏公平吗？请说明理由．
相关试题
