【题目】某校组织八年级师生共420人参观纪念馆,学校联系租车公司提供车辆,该公司现有A,B两种座位数不同的车型,如果租用A种车3辆,B种车5辆,则空余15个座位:如果租用A种车5辆,B种车3辆,则有15个人没座位
(1)求该公司A,B两种车型各有多少个座位?
(2)若A种车型的日租金为260元辆,B种车型的日租金为350元辆,怎样租车能使得座位恰好坐满且租金最少?最少租金是多少?(请直接写出答案)
参考答案:
【答案】(1)公司A、B两种车型各有45个座位和60个座位;(2)租该公司A、B两种车型各有8辆和1辆租金最少,最少租金为2430元.
【解析】
(1)设公司A、B两种车型各有x个座位和y个座位,由题意可列出方程组,求解即可;
(2)公司A、B两种车型各有a辆和b辆,租金为w元,由题意可列方程,即可求w=﹣![]() a+2450,即可求最少租金.
a+2450,即可求最少租金.
解:(1)设公司A、B两种车型各有x个座位和y个座位,
根据题意得:![]()
解得![]()
答:公司A、B两种车型各有45个座位和60个座位,
(2)设公司A、B两种车型各有a辆和b辆,租金为w元,
根据题意得:![]()
∴w=﹣![]() a+2450
a+2450
∵45a+60b=420
∴a=![]()
∵a,b为正整数
∴b=1,a=8,
b=4,a=4
∴当a=8时,w的值最小,即W=﹣20+2450=2430
∴租该公司A、B两种车型各有8辆和1辆租金最少,最少租金为2430元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F
的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F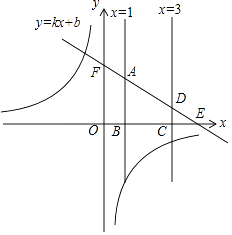
(1)当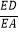 =
=  且△OFE的面积等于
且△OFE的面积等于 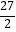 时,求这个一次函数的解析式;
时,求这个一次函数的解析式;
(2)在(1)的条件下,根据函数图象,试求不等式 >kx+b的解集.
>kx+b的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
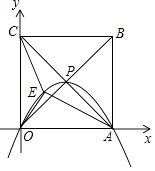
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: =
= 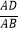 ;
;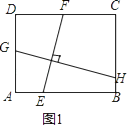
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 =
= 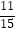 ,则
,则 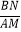 的值为;
的值为;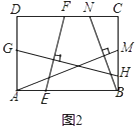
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求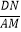 的值.
的值.
-
科目: 来源: 题型:
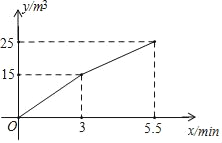
查看答案和解析>>【题目】某种水泥储存罐的容量为25m3,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3min后,再打开输出口,匀速向运输车输出水泥,又经过2.5min水泥储存罐注满.已知水泥储存罐内的水泥量y(m3)与时间x(min)之间的函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量;
(2)当3≤x≤5.5时,求y与x之间的函数关系式;
(3)水泥储存罐每分钟向运输车输出的水泥量是多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD为⊙O的内接四边四边形,已知∠BOD=100°,则∠BCD 的度数为( )

A.50°
B.80°
C.100°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 ,给出下列结论:
,给出下列结论:①
 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

