【题目】如图,在平面直角坐标系中,以点M(0,3)为圆心、5为半径的圆与x轴交于点A、B(点A在点B的左侧),与y轴交于点C、D(点C在点D的上方),经过B、C两点的抛物线的顶点E在第二象限.
(1)、求点A、B两点的坐标.
(2)、当抛物线的对称轴与⊙M相切时, 求此时抛物线的解析式.
(3)、连结AE、AC、CE,若![]() .①求点E坐标;②在直线BC上是否存在点P,使得以点B、M、
.①求点E坐标;②在直线BC上是否存在点P,使得以点B、M、
P为顶点的三角形和△ACE相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
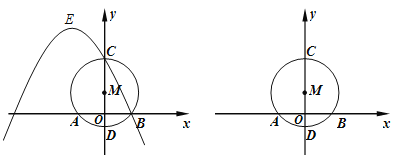
参考答案:
【答案】(1)、A(-4,0);B(4,0);(2)、![]() ;(3)、E
;(3)、E![]() ;P
;P![]() .
.
【解析】
试题分析:(1)、连接AM,根据题意得出AM=5,OM=3,则OA=0B=4,求出点坐标;(2)、设出函数解析式,根据题意得c=8,将点B的坐标代入找出b和a的关系式,求出直线的对称轴;根据切线的性质得出对称轴为x=-5,求出a和b的值;(3)、根据∠ACO和∠CAE的正切值得出两个角相等,根据点A在对称轴上,则可得出对对称轴为直线x=-4,求出a的值,然后求出顶点坐标.
试题解析:(1)、连结M A,由题意得:AM=5,OM=3,则OA=4,同理得OB=4,
∴点A、点B的坐标分别是(-4,0)、(4,0)
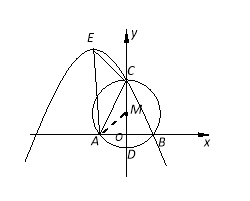
(2)设经过B、C两点的抛物线解析式为y=ax2+bx+c(a≠0),
∴c=8,0=16a+4b+8,∴b=-4a-2; 此时,y=ax2+(-4a-2)x+8(a≠0),
它的对称轴是直线:x=![]() =
=![]() ;
;
又∵抛物线的顶点E在第二象限且该抛物线的对称轴与⊙M相切, 则![]() =-5,∴a=
=-5,∴a=![]() ,b=
,b=![]() ,
,
∴抛物线的解析式为![]()
(3)、①在Rt△AOC中 tan∠ACO=![]() ,而tan∠CAE=
,而tan∠CAE=![]()
∴∠CAE=∠ACO,所以AE∥CO,即点A在抛物线的对称轴上
又∵y=ax2+(-4a-2)x+8,∴![]() ,∴a=
,∴a=![]() ;∴
;∴![]()
![]()
∴E![]()
②在直线BC上存在点P,使得以点B、M、P为顶点的三角形和△ACE相似,点P的坐标为![]()
-
科目: 来源: 题型:
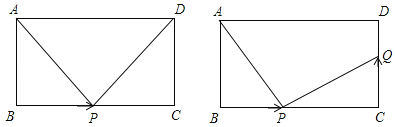
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3).点B在x轴上.将△AOB绕点A逆时针旋转90°得到△AEF,点0,B对应点分别是E,F。
(1)、若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E.F的坐标;
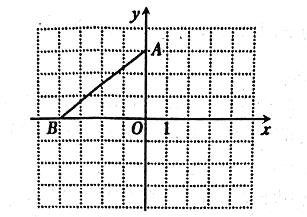
(2)、依此旋转,若要点F落在x轴上方时,试写出一个符合条件的点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB,CD为直线,DF交AB于E,EG交CD于O.若∠BEF=124°,∠D=56°,∠DEO=60°,则∠C0E的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的各组线段中,能够组成直角三角形的是 ( )
A.5,6,7 B.5,11,12 C.7,20,25 D.8,15,17
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x、y为有理数,现规定一种新运算“※”,满足x※y=xy+1,则2※4的值为 .
-
科目: 来源: 题型:
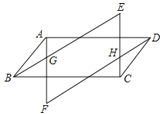
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.
相关试题

