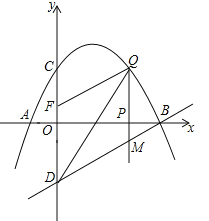
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
【解析】
(1)待定系数法求解可得;
(2)先利用待定系数法求出直线BD解析式为y=![]() x﹣2,则Q(m,﹣
x﹣2,则Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),将点C(0,2)代入,得:﹣4a=2,解得:a=﹣![]() ,则抛物线解析式为y=﹣
,则抛物线解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由题意知点D坐标为(0,﹣2),设直线BD解析式为y=kx+b,将B(4,0)、D(0,﹣2)代入,得:![]() ,解得:
,解得: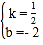 ,∴直线BD解析式为y=
,∴直线BD解析式为y=![]() x﹣2.
x﹣2.
∵QM⊥x轴,P(m,0),∴Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),则QM=﹣
m﹣2),则QM=﹣![]() m2+
m2+![]() m+2﹣(
m+2﹣(![]() m﹣2)=﹣
m﹣2)=﹣![]() m2+m+4.
m2+m+4.
∵F(0,![]() )、D(0,﹣2),∴DF=
)、D(0,﹣2),∴DF=![]() .
.
∵QM∥DF,∴当﹣![]() m2+m+4=
m2+m+4=![]() 时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在
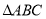 中,
中,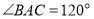 ,
,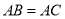 ,
,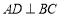 ,垂足为点
,垂足为点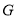 ,且
,且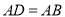 ,连接
,连接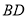 .
.(1)如图①,求证:
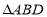 是等边三角形;
是等边三角形;
(2)如图①,若点
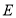 、
、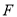 分别为
分别为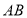 ,
,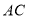 上的点,且
上的点,且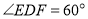 ,求证:
,求证: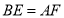 ;
;(3)利用(1)(2)中的结论,思考并解答:如图②,
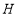 为
为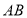 上一点,连结
上一点,连结 ,当
,当 时,线段
时,线段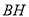 ,
,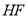 ,
,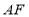 之间有何数量关系,给出证明.
之间有何数量关系,给出证明.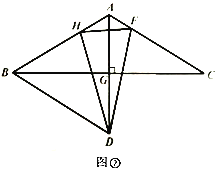
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图2211抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)抛物线线上是否存在一点P,使
 ,若存在,请求出点的坐标;若不存在请说明理由.
,若存在,请求出点的坐标;若不存在请说明理由.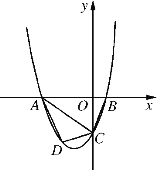
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=
 (BC+BF).
(BC+BF).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A.3B.4C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
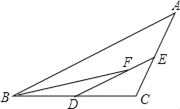
A. 1B. 2C. 3D. 4
相关试题

