搜索
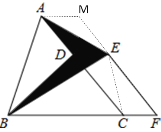
【题目】如图，已知△ABC的面积为24，点D在线段AC上，点F在线段BC的延长线上，且BF＝4CF，四边形DCFE是平行四边形，则图中阴影部分的面积为（ ）
A.3B.4C.6D.8
参考答案：
【答案】D
【解析】
连接EC，过A作AM∥BC交FE的延长线于M，求出平行四边形ACFM，根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等，△ADE的面积和△AME的面积相等，推出阴影部分的面积等于平行四边形ACFM的面积的一半，求出CF×hCF的值即可．
连接DE、EC，过A作AM∥BC交FE的延长线于M，
∵四边形CDEF是平行四边形，
∴DE∥CF，EF∥CD，
∴AM∥DE∥CF，AC∥FM，
∴四边形ACFM是平行四边形，
∵△BDE边DE上的高和△CDE的边DE上的高相同，
∴△BDE的面积和△CDE的面积相等，
同理△ADE的面积和△AME的面积相等，
即阴影部分的面积等于平行四边形ACFM的面积的一半，是
×CF×hCF，
∵△ABC的面积是24，BC＝3CF
∴BC×hBC＝×3CF×hCF＝24，
∴CF×hCF＝16，
∴阴影部分的面积是×16＝8，
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图2211抛物线y＝ax2＋2ax＋c(a>0)与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.
（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）抛物线线上是否存在一点P,使
，若存在，请求出点的坐标；若不存在请说明理由.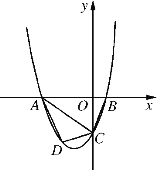
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线经过点A（-1,0），B（4,0）C（0,2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线
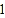交抛物线于点Q，交直线BD于点M．（1）求该抛物线所表示的二次函数的表达式；
（2）已知点F（0，
），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，AB=BC，BD⊥AC于点D；CE平分∠ACB，交AB于点E，交BD于点F．
（1）求证：△BEF是等腰三角形；
（2）求证：BD=
（BC+BF）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，D、E分别是BC、AC中点，BF平分∠ABC．交DE于点F．AB＝8，BC＝6，则EF的长为( )
A. 1B. 2C. 3D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=a（x2﹣4mx﹣12m2）（其中a、m是常数，且a＞0，m＞0）的图象与x轴分别交于点A、B（点A位于点B的左侧），与y轴交于C（0，﹣6），点D在二次函数的图象上，CD∥AB，连接AD，过点A作射线AE交二次函数的图象于点E，AB平分∠DAE．
（1）用含m的代数式表示a；
（2）求证：
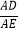为定值；（3）设该二次函数图象的顶点为F，连接FC并延长交x轴的负半轴于点G，判断以线段GF、AD、AE的长度为三边长的三角形的面积是否能为24（
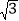+1）m2﹣48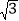m﹣72+24，能则求出m；不能则说明理由．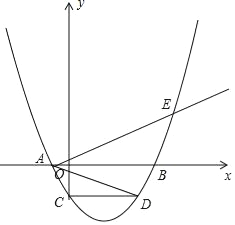
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，∠BAD的平分线交CD于点G，AD＝AE．若AD＝5，DE＝6，则AG的长是（ ）
A. 6B. 8C. 10D. 12
相关试题
