搜索
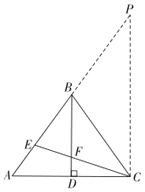
【题目】如图，在△ABC中，∠ABC=90°，AB=BC，BD⊥AC于点D；CE平分∠ACB，交AB于点E，交BD于点F．
（1）求证：△BEF是等腰三角形；
（2）求证：BD=
（BC+BF）．
参考答案：
【答案】（1）证明见解析（2）证明见解析
【解析】试题分析： 
根据
以及
即可得到
即可判定
是等腰三角形；
延长AB至M，使得BM=AB，连接CM，根据三角形中位线定理可得
再根据
，可得
进而得出
试题解析： 
在△ABC中，AB=BC，BD⊥AC于点D，
∴∠ABD=∠CBD，AD=CD，
∵CE平分∠ACB，
∴BE=BF，
∴△BEF是等腰三角形；
如图，延长AB至M，使得BM=AB，连接CM，
∴BC=BM，
由
得，∠BEF=∠BFE，BE=BF，
∴∠BFE=∠MCE=∠BEF，
∴EM=MC,
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.线段AB和线段BA表示的不是同一条线段B.x2y的系数是1，次数是2
C.多项式4x2y﹣2xy+1的次数是3D.射线AB和射线BA表示的是同一条射线
-
科目： 来源： 题型：
查看答案和解析>>【题目】若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式：①（a﹣b）2；②ab+bc+ca；③a2b+b2c+c2a．其中是完全对称式的是（ ）
A. ①②③ B. ①③ C. ②③ D. ①②
-
科目： 来源： 题型：
查看答案和解析>>【题目】在“长方体、圆柱、圆锥 ”三种几何体中，用一个平面分别去截三种几何体，则截面的形状可以截出长方形也可以截出圆形的几何体是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是某同学对多项式（x2－4x-3）（x2－4x+1）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y-3）（y+1）+4 （第一步）
= y2-2y+1 （第二步）
=（y-1）2 （第三步）
=（x2－4x-1）2 （第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式法 B．平方差公式法 C.完全平方公式法
（2）请你模仿以上方法尝试对多项式（x2+2x）（x2+2x+2）+1进行因式分解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数
和一次函数
，把
称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L．现有点A（2，0）和抛物线L上的点B（﹣1，n），请完成下列任务：【尝试】（1）当t=2时，抛物线
的顶点坐标为 ；（2）判断点A (填是或否)在抛物线L上；
（3）n的值是 ；
【发现】通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为 ．
【应用】二次函数
是二次函数
和一次函数
的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，为了测量某电线杆（底部可到达）的高度，准备了如下的测量工具：
①平面镜；②皮尺；③长为2米的标杆；④高为1.5m的测角仪（测量仰角、俯角的仪器），请根据你所设计的测量方案，回答下列问题：
（1）画出你的测量方案示意图，并根据你的测量方案写出你所选用的测量工具；
（2）结合你的示意图，写出求电线杆高度的思路．
相关试题
