搜索
【题目】已知，在
中，
，
，
，垂足为点
，且
，连接
.
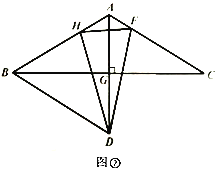
（1）如图①，求证：
是等边三角形；
（2）如图①，若点
、
分别为
，
上的点，且
，求证：
；
（3）利用（1）（2）中的结论，思考并解答：如图②，
为上一点，连结
，当
时，线段
，
，
之间有何数量关系，给出证明.
参考答案：
【答案】（1）详见解析；（2）详见解析；（3）
，理由详见解析.
【解析】
（1）根据等腰三角形三线合一定理，得到
，即可得到结论成立；
（2）由（1）得
，
，然后证明
，即可得到结论成立；
（3）在
上取一点
，连接
，使
.，由（2）得
，则
，
，然后得到
，即可得到.
（1）证明：∵
，
，
∴
，
∵
，
∴
，
∵
，
∴
是等边三角形；
（2）证明：∵是等边三角形，
∴，
∵
，
∴
，
在
与
中，
∴，
∴；
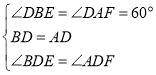
（3）；
理由如下：如图②，在上取一点，连接，使.
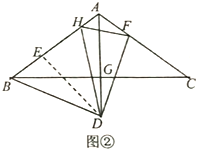
由（1）（2）可得，
∴，
在
和
中
∴
∴
∴；
-
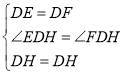
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两名学生参加数学素质测试（有四项），每项测试成绩采用百分制，成绩如表：
学生
数与代数
空间与图形
统计与概率
综合与实践
平均成绩
方差
甲
87
93
91
85
89
______
乙
89
96
91
80
______
______
（1）将表格中空缺的数据补充完整，根据表中信息判断哪个学生数学综合素质测试成绩更稳定？请说明理由.
（2）若数与代数、空间与图形、统计与概率、综合与实践的成绩按
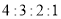，计算哪个学生数学综合素质测试成绩更好？请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间（s）满足二次函数关系，t与h的几组对应值如下表所示：
t（s）
0
0.5
1
1.5
2
…
h（m）
0
8.75
15
18.75
20
…
（1）求h与t之间的函数关系式（不要求写t的取值范围）；
（2）求小球飞行3s时的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我校图书馆大楼工程在招标时，接到甲乙两个工程队的投标书，每施工一个月，需付甲工程队工程款16万元，付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算，可有三种施工方案：
（1）甲队单独完成此项工程刚好如期完工；
（2）乙队单独完成此项工程要比规定工期多用3个月；
（3）若甲乙两队合作2个月，剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款，说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图2211抛物线y＝ax2＋2ax＋c(a>0)与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.
（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）抛物线线上是否存在一点P,使
，若存在，请求出点的坐标；若不存在请说明理由.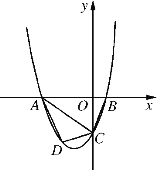
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线经过点A（-1,0），B（4,0）C（0,2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线
交抛物线于点Q，交直线BD于点M．（1）求该抛物线所表示的二次函数的表达式；
（2）已知点F（0，
），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？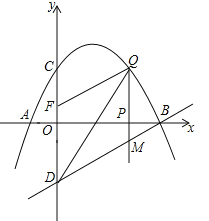
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，AB=BC，BD⊥AC于点D；CE平分∠ACB，交AB于点E，交BD于点F．
（1）求证：△BEF是等腰三角形；
（2）求证：BD=
（BC+BF）．
相关试题
