搜索
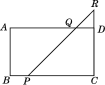
【题目】如图，在长方形ABCD中，AB＝4，BC＝7，点P是BC边上与点B不重合的动点，过点P的直线交CD的延长线于点R，交AD于点Q(点Q与点D不重合)，且∠RPC＝45°.设BP＝x，梯形ABPQ的面积为y，求y与x之间的函数关系式，并求出自变量x的取值范围．
参考答案：
【答案】y＝4x＋8(0<x<3)．
【解析】
由梯形面积公式S=
(AQ+BP)×AB，设BP=x，AB=4，需求得AQ，又∠RPC=45，AQ=AD-QD，QD=RD=RC-CD=PC-CD，由此得出y与x之间的函数关系；对于自变量x的取值范围，求临界条件Q与D重合时，BP=x=3，又Q与D不重合，故x＜3．
如图，过点D作DP′∥PQ，交BC于点P′，
则∠DP′C＝∠RPC＝45°，
∴P′C＝CD＝4，∴BP′＝3.∴BP＜3.
∵BP＝x，∴PC＝7－x.
在Rt△PCR中，∠C＝90°，
∠RPC＝45°，
∴CR＝PC＝7－x.
∴QD＝RD＝CR－CD
＝7－x－4
＝3－x，
∴AQ＝AD－QD
＝7－(3－x)
＝4＋x.
∴y＝ (BP＋AQ)·AB
＝ (x＋4＋x)×4
＝4x＋8(0<x<3)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A（3，0），与y轴交于点B（0，3），点P是x轴上一动点，过点P作x轴的垂线交抛物线于点C，交直线AB于点D，设P（x，0）．
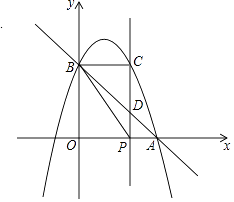
（1）求抛物线的函数表达式；
（2）当0＜x＜3时，求线段CD的最大值；
（3）在△PDB和△CDB中，当其中一个三角形的面积是另一个三角形面积的2倍时，求相应x的值；
（4）过点B，C，P的外接圆恰好经过点A时，x的值为 ． （直接写出答案） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与点A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F、D．
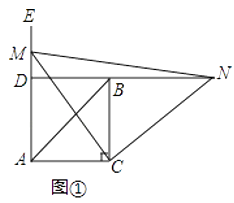
（1）问题发现：直接写出∠NDE=度；
（2）拓展探究：试判断，如图②当∠EAC为钝角时，其他条件不变，∠NDE的大小有无变化？请给出证明．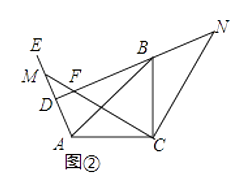
（3）如图③，若∠EAC=15°，BD=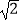
，直线CM与AB交于点G，其他条件不变，请直接写出AC的长．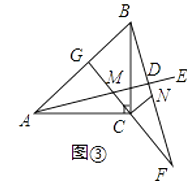
-
科目： 来源： 题型：
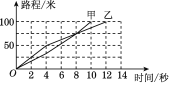
查看答案和解析>>【题目】甲、乙两人进行比赛的路程与时间的关系如图所示．
(1)这是一场________米比赛；
(2)前一半赛程内________的速度较快，最终________赢得了比赛；
(3)两人第________秒在途中相遇，相遇时距终点________米；
(4)甲在前8秒的平均速度是多少？甲在整个赛程的平均速度是多少？乙在前8秒的平均速度是多少？乙在整个赛程的平均速度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段．在连接两点所得的所有线段中任取一条线段，取到长度为
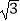的线段的概率为（ ）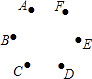
A.
B.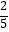
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】气温随着高度的升高而下降，下降的一般规律是从地面到高空11 km处(包括11 km)，每升高1 km气温下降6 ℃；高于11 km时，气温不再发生变化，地面的气温为20 ℃时，设高空中x km处的气温为y ℃.
(1)当0≤x≤11时，求y和x之间的关系式；
(2)画出气温随高度(包括高于11 km)变化的图像；
(3)在离地面4.5 km及14 km的高空处，气温分别是多少？
-
科目： 来源： 题型：
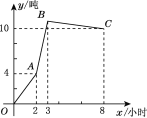
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车，每辆车只负责进货或出货，其中丙车每小时的运输量最多，乙车每小时的运输量最少，且乙车每小时的运输量为6吨．如图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图像，OA段只有甲、丙车工作，AB段只有乙、丙车工作，BC段只有甲、乙车工作．
(1)你能确定甲、乙、丙三辆车哪辆是出货车吗？并说明理由．
(2)若甲、乙、丙三辆车一起工作，一天工作8小时，则仓库的库存量增加多少？
相关试题
