【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.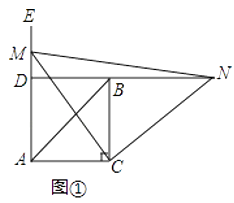
(1)问题发现:直接写出∠NDE=度;
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.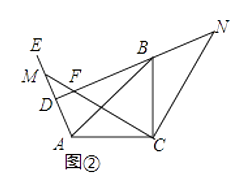
(3)如图③,若∠EAC=15°,BD= ![]() ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.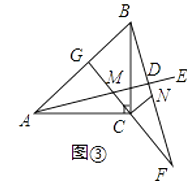
参考答案:
【答案】
(1)90
(2)解:∠NDE的大小不变,
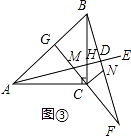
在△MAC和△NBC中,
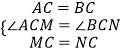 ,
,
∴△MAC≌△NBC,
∴∠N=∠AMC,
又∵∠MFD=∠NFC,
∴∠MDF=∠FCN=90°,
即∠NDE=90°
(3)解:AC=2,
在△MAC和△NBC中,
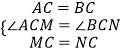 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=15°,
如图③,设BC与AD交于点H,
又∵∠AHC=∠BHD,
∴∠BDH=∠ACH=90°,
∴在Rt△ABD中,∠ABD=∠ABC+∠NBC=45°+15°=60°
∵BD= ![]() ,
,
∴AB=2 ![]() ,
,
∴AC=ABcos45°=2.
【解析】解:(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中,
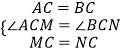 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,
∴∠NDE=90°.
所以答案是:90.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
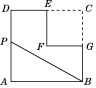
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图像大致为( )
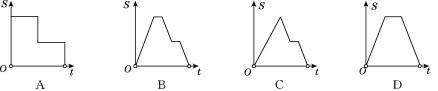
A. (A) B. (B) C. (C) D. (D)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某航空公司托运行李的费用y(元)与行李的质量x(千克)之间的关系,由图可以看出:
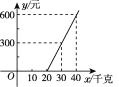
(1)当行李质量为30千克时,行李托运费是________元;
(2)当行李质量为________千克时,行李托运费是600元;
(3)每位旅客最多可以免费携带________千克的行李.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).
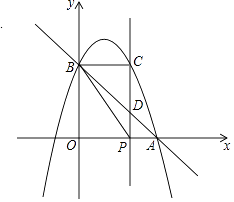
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 . (直接写出答案) -
科目: 来源: 题型:
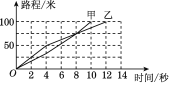
查看答案和解析>>【题目】甲、乙两人进行比赛的路程与时间的关系如图所示.
(1)这是一场________米比赛;
(2)前一半赛程内________的速度较快,最终________赢得了比赛;
(3)两人第________秒在途中相遇,相遇时距终点________米;
(4)甲在前8秒的平均速度是多少?甲在整个赛程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整个赛程的平均速度是多少?
-
科目: 来源: 题型:
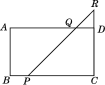
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=4,BC=7,点P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点R,交AD于点Q(点Q与点D不重合),且∠RPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
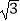 的线段的概率为( )
的线段的概率为( )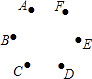
A.
B.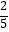
C.
D.
相关试题

