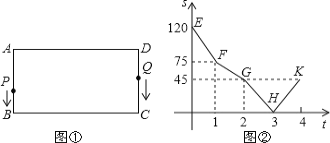
【题目】如图①,在矩形ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A匀速运动,到达点A后停止。若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB→BC→CD上相距的路程S(cm)与时间t(s)之间的函数关系图象。
(1)请解释图中点H的实际意义?
(2)求P、Q两点的运动速度;
(3)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值。
参考答案:
【答案】(1)P,Q两点相遇 (2)![]()
(3)当![]() 或5s或8s时,△PCQ为等腰三角形
或5s或8s时,△PCQ为等腰三角形
【解析】
(1)根据P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象得出H点时两点相遇;
(2)利用函数图象得出当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留,只有P点运动,再利用纵坐标的值得出P点和Q点运动速度;
(3)根据Q,P的位置不同,进行分类讨论得出答案即可
1)图中点H的实际意义:P、Q两点相遇
(2)由函数图象得出,当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒,只有P点运动,此时纵坐标的值由75下降到45,故P点运动速度为:30cm/s,再根据E点到F点S的值由120变为75,根据P点速度,得出Q点速度为120-75-30=15(cm/s)
即P点速度为30cm/s,Q点速度为15cm/s
(3)如图1所示
当QP=PC,此时![]() QC=BP,即30-30t=
QC=BP,即30-30t=![]() (30-15t),解得:t=
(30-15t),解得:t=![]() ,
,
故当时间t=![]() s时,△PCQ为等腰三角形
s时,△PCQ为等腰三角形
如图2所示,
当D,P重合,QD=QC时
Q为AB中点,则运动时间为:(15+60+30)÷15+1=8(s),
故当时间t=8s时,△PCQ为等腰三角形
若PC=CQ
故90-30t=30-15t
解得t=4
则4+1=5(S)
综上所述:t=![]() 或t=5或t=8秒时,△PO为等腰三角形
或t=5或t=8秒时,△PO为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1),下列结论:① 2a+b>0;② abc<0;③ 若OC=2OA,则2b-ac = 4;④ 3a﹣c<0,其中正确的个数是( )
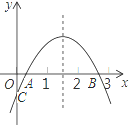
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“五一”期间,某公司组织318名员工到雷山西江千户苗寨旅游,旅行社承诺每辆车安排有一名随团导游,并为此次旅行安排8名导游,现打算同时租甲、乙两种客车,其中甲种客车每辆载客45人,乙种客车每辆载客30人.
(1)请帮助旅行社设计租车方案.
(2)若甲种客车租金为800元/辆,乙种客车租金为600元/辆,旅行社按哪种方案租车最省钱?此时租金是多少?
(3)旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游随团导游,为保证所租的每辆车安排有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
-
科目: 来源: 题型:
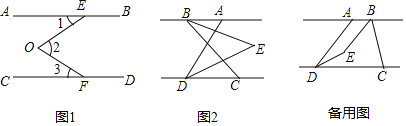
查看答案和解析>>【题目】已知AB∥CD.
(1)如图1,EOF是直线AB、CD间的一条折线,猜想∠1、∠2、∠3的数量关系,并说明理由;
(2)如图2,若点C在点D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DF所在直线交于点E,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示);
(3)在(2)的前提下将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)+3+(-5)
(2)-89-11
(3)(﹣5.5)+(﹣3.2)﹣(﹣2.5)﹣4.8
(4)17﹣(﹣8)×(﹣2)+4×(﹣3)
(5)(-32
 )-[5
)-[5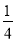 -(+3
-(+3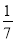 )+(-5
)+(-5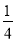 )+(-2
)+(-2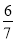 )]
)](6)(
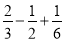 )×(﹣12)
)×(﹣12) -
科目: 来源: 题型:
查看答案和解析>>【题目】在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数y(次/分)是这个人年龄x(岁)的一次函数。
(1)根据图中信息,求在正常情况下,y关于x的函数关系式;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.

相关试题

