【题目】在“五一”期间,某公司组织318名员工到雷山西江千户苗寨旅游,旅行社承诺每辆车安排有一名随团导游,并为此次旅行安排8名导游,现打算同时租甲、乙两种客车,其中甲种客车每辆载客45人,乙种客车每辆载客30人.
(1)请帮助旅行社设计租车方案.
(2)若甲种客车租金为800元/辆,乙种客车租金为600元/辆,旅行社按哪种方案租车最省钱?此时租金是多少?
(3)旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游随团导游,为保证所租的每辆车安排有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
参考答案:
【答案】(1)见解析;(2)租甲种客车6辆;租乙种客车2辆,所需付费最少为6000元;
(3)见解析.
【解析】
(1)设租甲种客车x辆,则租乙种客车(8-x)辆,依题意关系式为:45x+30(8-x)≥318+8,
(2)分别算出各个方案的租金,比较即可;
(3)根据设同时租65座、45座和30座的大小三种客车各x辆,y辆,(7-x-y)辆,列出二元一次方程求解即可.
(1)设租甲种客车x辆,则租乙种客车(8﹣x)辆,
依题意,得45x+30(8﹣x)≥318+8,
解得x≥5![]() ,
,
∵打算同时租甲、乙两种客车,
∴x<8,即5![]() ≤x<8,
≤x<8,
x=6,7,
有两种租车方案:
租甲种客车6辆,则租乙种客车2辆,
租甲种客车7辆,则租乙种客车1辆;
(2)∵6×800+2×600=6000元,7×800+1×600=6200元,
∴租甲种客车6辆;租乙种客车2辆,所需付费最少为6000(元);
(3)设同时租65座、45座和30座的大小三种客车各x辆,y辆,(7﹣x﹣y)辆,
根据题意得出:65x+45y+30(7﹣x﹣y)=318+7,
整理得出:7x+3y=23,
1≤x<7,1≤y<7,1≤7﹣x﹣y<7,
故符合题意的有:x=2,y=3,7﹣x﹣y=2,
租车方案为:租65座的客车2辆,45座的客车3辆,30座的2辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2x+c经过点A(0,3)、B(﹣1,0),请解答下列问题:
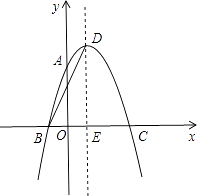
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接四边形各边中点,所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平面直角坐标系内,点A(a,0),B(b,2),C(0,2),且a、b是方程组
 的解,求:
的解,求:(1)a、b的值.
(2)过点E(6,0)作PE∥y轴,点Q(6,m)是直线PE上一动点,连QA、QB,试用含有m的式子表示△ABQ的面积.
(3)在(2)的条件下.当△ABQ的面积是梯形OABC面积一半时,求Q点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )

A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD
相关试题

