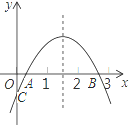
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1),下列结论:① 2a+b>0;② abc<0;③ 若OC=2OA,则2b-ac = 4;④ 3a﹣c<0,其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】试题解析:①∵抛物线的开口向下,
∴a<0.
∵抛物线的对称轴-![]() >1,
>1,
∴b>-2a,即2a+b>0,①成立;
②∵b>-2a,a<0,
∴b>0,
∵抛物线与y轴的交点在y轴的负半轴,
∴c<0,
∴abc>0,②错误;
③点A的横坐标为![]() ,点C的纵坐标为c,
,点C的纵坐标为c,
∵OC=2OA,
∴-c=![]() ,整理得:2b-ac=4,③成立;
,整理得:2b-ac=4,③成立;
④∵抛物线的对称轴1<-![]() <2,
<2,
∴-2a<b<-4a,
∵当x=1时,y=a+b+c>0,
∴a-4a+c>0,即3a-c<0,④正确.
综上可知正确的结论有3个.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中错误的是( )
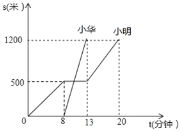
A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米/分
C.小明跑步的平均速度是100米/分
D.小华到学校的时间是7:55
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了“乘方”运算,下面介绍一种新运算,即“对数”运算.
定义:如果
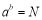 (a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作
(a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作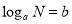 .
.例如:因为
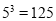 ,所以
,所以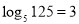 ;因为
;因为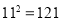 ,所以
,所以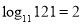 .
.根据“对数”运算的定义,回答下列问题:
(1)填空:
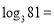 ,
,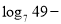
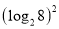 = .
= .(2)已知m,n为整数,且|m-2|+|m-n|=
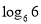 ,求m+n的值.
,求m+n的值.(3) 对于“对数”运算,小明同学认为有“
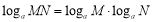 (a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请说明理由;如果不正确,请举出一个反例加以说明,并写出正确的结论.
(a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请说明理由;如果不正确,请举出一个反例加以说明,并写出正确的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上,点O为原点,点A表示的数为9,动点B,C在数轴上移动,且总保持BC=2(点C在点B右侧),设点B表示的数为m.
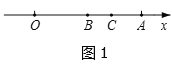

(1) 如图1,当B,C在线段OA上移动时,
① 若B为OA中点,则AC= ;
② 若B,C移动到某一位置时,恰好满足AC=OB,求此时m的值;
(2) 当线段BC沿射线AO方向移动时,若存在AC-OB=
 AB,求满足条件的m值.
AB,求满足条件的m值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块直角三角尺的直角顶点O叠放在一起.
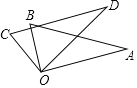
(1)如果∠BOD=60°,那么∠AOC= ,如果∠AOC=130°,那么∠BOD= .
(2)猜想∠AOC与∠BOD的数量关系,并说明理由.
-
科目: 来源: 题型:
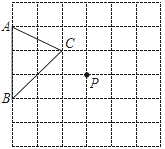
查看答案和解析>>【题目】如图,在正方形网格中,每一小正方形的边长为1,格点△ABC(三个顶点在相应的小正方形的顶点处)在如图所示的位置:
(1) △ABC的面积为___________ 直接写出)
(2) 在网格中画出线段AB绕格点P顺时针旋转90°之后的对应线段A1B1(点A1对应点A)
(3) 在(2)的基础上直接写出
 =___________
=___________ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
相关试题

