【题目】如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)在点Q从B到A的运动过程中,
①当t=时,PQ⊥AC;
(2)②求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l.
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.
参考答案:
【答案】
(1)![]()
(2)
解:如图1所示,过点P作PH⊥AB于点H,

AP=t,AQ=3﹣t,
则∠AHP=∠ABC=90°,
∵∠PAH=∠CAB,
∴△AHP∽△ABC,
∴ ![]() ,
,
∵AP=t,AC=5,BC=4,
∴PH= ![]() t,
t,
∴S= ![]() (3﹣t)
(3﹣t) ![]() t,
t,
即S=﹣ ![]() t2+
t2+ ![]() t,t的取值范围是:0<t<3.
t,t的取值范围是:0<t<3.
(3)
解:①如图2,线段PQ的垂直平分线为l经过点A,则AP=AQ,
即3﹣t=t,
∴t=1.5,
∴AP=AQ=1.5;
延长QP交AD于点E,过点Q作QO∥AD交AC于点O,

则△AQO∽△ABC,
∴ ![]() ,
,
∴AO= ![]() AC=
AC= ![]() ,QO=
,QO= ![]() BC=2,
BC=2,
∴PO=AO﹣AP=1.
∵OQ∥BC∥AD,
∴△APE∽△OPQ
∴ ![]() ,
,
∴AE= ![]() QO=3.
QO=3.
②(ⅰ)如图3,当点Q从B向A运动时l经过点B,

BQ=CP=AP=t,∠QBP=∠QAP
∵∠QBP+∠PBC=90°,∠QAP+∠PCB=90°
∴∠PBC=∠PCB CP=BP=AP=t
∴CP=AP= ![]() AC=
AC= ![]() ×5=2.5∴t=2.5.
×5=2.5∴t=2.5.
(ⅱ)如图4,当点Q从A向B运动时l经过点B;

BP=BQ=3﹣(t﹣3)=6﹣t,AP=t,PC=5﹣t,
过点P作PG⊥CB于点G,则PG∥AB,
∴△PGC∽△ABC,
∴ ![]() ,
,
∴PG= ![]() AB=
AB= ![]() (5﹣t),CG=
(5﹣t),CG= ![]() BC=
BC= ![]() (5﹣t),
(5﹣t),
∴BG=4﹣ ![]() (5﹣t)=
(5﹣t)= ![]() t,
t,
由勾股定理得:BP2=BG2+PG2,
即(6﹣t)2=( ![]() t)2+[
t)2+[ ![]() (5﹣t)]2,
(5﹣t)]2,
解得:t= ![]() ;
;
综上所述:存在t的值,使得直线l经过点B,t的值是2.5或 ![]() .
.
【解析】解:(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴AC= ![]() =
= ![]() =5,
=5,
∵PQ⊥AC,
∴∠APQ=90°=∠B,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,
∴ ![]() ,
,
即 ![]() ,
,
解得:t= ![]() ,
,
即t= ![]() 时,PQ⊥AC,
时,PQ⊥AC,
所以答案是: ![]() ;
;
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
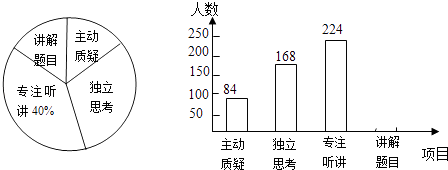
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.

(1)判断直线CA与⊙O的位置关系,并说明理由;
(2)若AB= ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π). -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
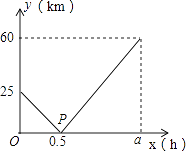
(1)填空:A、C两港口间的距离为km,a=;
(2)求y与x的函数关系式,并请解释图中点P的坐标所表示的实际意义;
(3)在B岛有一不间断发射信号的信号发射台,发射的信号覆盖半径为15km,求该海巡船能接受到该信号的时间有多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
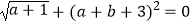 ,ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
,ABCD的边AD与y轴交于点E,且E为AD中点,双曲线 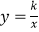 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线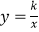 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,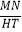 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则
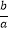 的值等于 .
的值等于 . 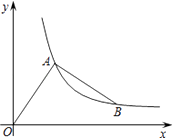
-
科目: 来源: 题型:
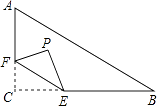
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
相关试题

