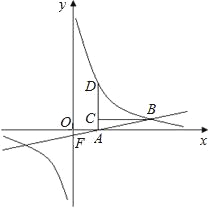
【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
参考答案:
【答案】(1)双曲线解析式为![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据点C的坐标,利用比值关系求出D点的坐标,然后根据待定系数法求出反比例函数的解析式;
(2)根据解析式求出B点的坐标,用A点坐标求出直线AB的解析式,再求出F点的坐标,最后根据三角形的面积求解.
试题解析:(1)∵点C的坐标为(3,2);
∴OA=3,AC=2.
∵AC:AD=1:3,
∴AD=6,
∴点D的坐标为(3,6) ;
设该双曲线的解析式为![]() ;
;
∴k=3×6=18,
∴该双曲线的解析式为![]() ;
;
(2)设直线AB的解析式为y=kx+b(k≠0);
∵B点的纵坐标为2,且B点在双曲线![]() 上,
上,
∴![]()
∴x=9
∴B点的坐标为(9,2),A点的坐标为(3,0);
∴![]()
解之得: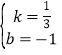
∴直线AB的解析式为y=![]() x-1;
x-1;
∵直线AB与y轴的交点为F;
∴F点的坐标为(0,-1),
∴OF=1,
∴△OFA的面积=![]() ×OA·OF=
×OA·OF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB//CD,(1)如图,若 E 为 DC 延长线上一点,AF、CG 分别为∠BAC、∠ACE 的平分线, 求证:AF//CG.

(2)若 E 为线段 DC 上一点(E 不与 C 重合),AF、CG 分别为∠BAC、∠ACE
的平分线,画出图形,试判断 AF,CG 的位置关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于气温,有的地方用摄氏度表示,有的地方用华氏温度表示,从温度计上可以看出,摄氏温度
 与华氏温度
与华氏温度 有如下对应的关系.下列说法不正确的是( )
有如下对应的关系.下列说法不正确的是( )
A. 摄氏温度
 与华氏温度
与华氏温度 都是变量,摄氏温度
都是变量,摄氏温度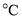 是自变量,华氏温度
是自变量,华氏温度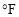 是因变量
是因变量B. 随着摄氏温度
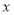 的逐渐升高,华氏温度
的逐渐升高,华氏温度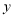 也逐新升高
也逐新升高C. 摄氏温度每升高
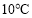 ,华氏温度升高
,华氏温度升高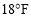
D. 当摄氏温度为
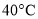 时,华氏温度为
时,华氏温度为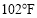
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1, ∠ABD1与∠ACD1的角平分线交于点D2,依次类推,∠ABD4与∠ACD4 的角平分线交于点D5,则∠BD5C的度数是( )

A. 56°;B. 60°;C. 68°;D. 94°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是
是 的中点,
的中点, ,
, ,
, 平分
平分 ,下列结论:①
,下列结论:① ;②
;② ;③
;③ ;④
;④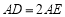 ,四个结论中成立的是__________.
,四个结论中成立的是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
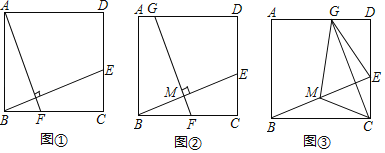
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
相关试题

