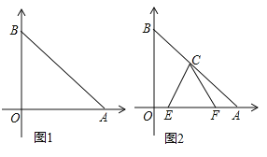
【题目】已知点A、B分别在x轴和y轴上,OA=OB,点C为AB的中点,AB=![]()
(1) 如图1,求![]() 的面积.
的面积.
(2) 如图2,E、F分别为![]() 上的动点,且∠ECF=45°,求证:
上的动点,且∠ECF=45°,求证:![]()
参考答案:
【答案】(1)72(2)见解析
【解析】
(1)根据等腰直角三角形的性质即可求解;(2)连接OC,在OB上截取OM=AF,连接CM、ME,通过证得△ACF≌△OCM,得出CM=AF,∠OCM=∠ACF,再通过角度的计算得出∠ECM=∠ECF=45°,得到△ECF≌△ECM,得出ME=EF,然后在Rt△MOE中通过勾股定理证明.
(1)∵OA⊥OB
∴OA2+OB2=AB2
∵OA=OB, AB=![]()
∴2OA2 =AB2
∴AO=BA=12
故S△ABO=![]()
(2)连接OC,在OB上截取OM=AF,连接CM、ME,如图2,
∵△AOB, △COA, △OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC,
在△ACF和△OCM中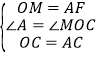
∴△ACF≌△OCM,
∴CM=CF,∠OCM=∠ACF,
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF
在△ECF和△ECM中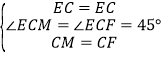
∴△ECF≌△ECM,∴ME=EF,
在Rt△MOE中,∠MOE=90°,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

-
科目: 来源: 题型:
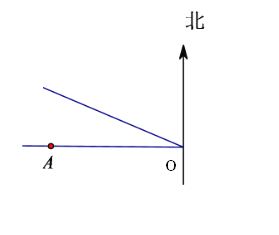
查看答案和解析>>【题目】某台风中心位于O点,台风中心以
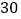
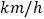 的速度向北偏西
的速度向北偏西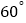 方向移动,在半径
方向移动,在半径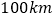 的范围内将受影响,城市A在O点正西方向与O点相距
的范围内将受影响,城市A在O点正西方向与O点相距 处,试问:
处,试问: (1)
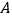 市是否会受此台风影响,并说明理由;
市是否会受此台风影响,并说明理由;(2)如受影响,则受影响的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D为边BC上一点,请回答下列问题:

(1)如图1,若∠DAC=∠B,△ABC的角平分线CE交AD于点F,试说明∠AEF=∠AFE;
(2)在(1)的条件下,如图2,△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P,若∠P=26°,猜想∠CFD的度数,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )

A. 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B. 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C. 用计算器产生1和2两个随机整数,1代表正面,2代表反面
D. 转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面
-
科目: 来源: 题型:
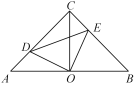
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,O是AB的中点,点D在AC上,点E在BC上,且∠DOE=90°.则下列结论:①OA=OB=OC;②CD=BE;③△ODE是等腰直角三角形;④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
相关试题

