【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
参考答案:
【答案】(1)见解析(2)BD=2
【解析】解:(1)证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°。
∵在Rt△ACD和Rt△AED中,![]() ,
,
∴Rt△ACD≌Rt△AED(HL)。
(2)∵Rt△ACD≌Rt△AED ,CD=1,∴DC=DE=1。
∵DE⊥AB,∴∠DEB=90°。
∵∠B=30°,∴BD=2DE=2。
(1)根据角平分线性质求出CD=DE,根据HL定理求出另三角形全等即可。
(2)求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】用恰当的方法解下列方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年6月1日起,国家实施了中央财政补贴条例支持高效节能电器的推广使用,某款定速空调在条例实施后,每购买一台,客户可获财政补贴200元,若同样用11万元所购买的此款空调数台,条例实施后比实施前多10%.求条例实施前此款空调的单价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

-
科目: 来源: 题型:
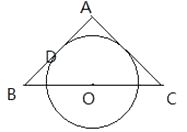
查看答案和解析>>【题目】如图所示,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于D点. 求证:AC是⊙O的切线.
相关试题

