【题目】在△ABC中,点D为边BC上一点,请回答下列问题:

(1)如图1,若∠DAC=∠B,△ABC的角平分线CE交AD于点F,试说明∠AEF=∠AFE;
(2)在(1)的条件下,如图2,△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P,若∠P=26°,猜想∠CFD的度数,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)∠CFD=64°,理由见解析.
【解析】
(1)利用角平分线的定义可得出∠ECB=∠ACE,结合∠B=∠FAC可得出∠B+∠ECB=∠FAC+∠ACE,由三角形外角的性质可得出∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,进而可得出∠AEF=∠AFE;
(2)由∠ACE=![]() ∠ACB,∠ACP=
∠ACB,∠ACP=![]() ∠ACQ,可得出∠ECP=90°,进而可得出∠P+∠AEC=90°,结合(1)的结论及对顶角相等可得出∠P+∠CFD=90°,代入∠P=26°即可求出∠CFD的度数.
∠ACQ,可得出∠ECP=90°,进而可得出∠P+∠AEC=90°,结合(1)的结论及对顶角相等可得出∠P+∠CFD=90°,代入∠P=26°即可求出∠CFD的度数.
解:(1)∵CE平分∠ACB,
∴∠ECB=∠ACE,
∵∠B=∠FAC,
∴∠B+∠ECB=∠FAC+∠ACE.
又∵∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,
∴∠AEF=∠AFE.
(2)∠CFD=64°,理由如下:
∵∠ACE=![]() ∠ACB,∠ACP=
∠ACB,∠ACP=![]() ∠ACQ,
∠ACQ,
∴∠ECP=∠ACE+∠ACP=![]() (∠ACB+∠ACQ)=90°,
(∠ACB+∠ACQ)=90°,
∴∠P+∠AEC=90°.
∵∠AEF=∠AFE=∠CFD,
∴∠P+∠CFD=90°.
∵∠P=26°,
∴∠CFD=64°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-
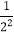 )(1-
)(1- )(1-
)(1-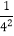 )…(1-
)…(1-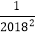 )(1-
)(1- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

-
科目: 来源: 题型:
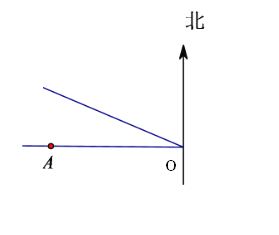
查看答案和解析>>【题目】某台风中心位于O点,台风中心以
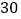
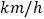 的速度向北偏西
的速度向北偏西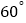 方向移动,在半径
方向移动,在半径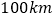 的范围内将受影响,城市A在O点正西方向与O点相距
的范围内将受影响,城市A在O点正西方向与O点相距 处,试问:
处,试问: (1)
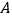 市是否会受此台风影响,并说明理由;
市是否会受此台风影响,并说明理由;(2)如受影响,则受影响的时间有多长?
-
科目: 来源: 题型:
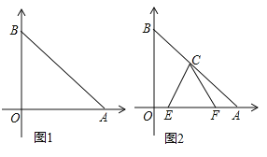
查看答案和解析>>【题目】已知点A、B分别在x轴和y轴上,OA=OB,点C为AB的中点,AB=
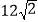
(1) 如图1,求
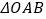 的面积.
的面积.(2) 如图2,E、F分别为
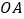 上的动点,且∠ECF=45°,求证:
上的动点,且∠ECF=45°,求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )

A. 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B. 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C. 用计算器产生1和2两个随机整数,1代表正面,2代表反面
D. 转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面
-
科目: 来源: 题型:
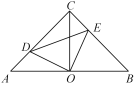
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,O是AB的中点,点D在AC上,点E在BC上,且∠DOE=90°.则下列结论:①OA=OB=OC;②CD=BE;③△ODE是等腰直角三角形;④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).
相关试题

