【题目】(1)请用两种不同的方法列代数式表示图1阴影部分的面积.
方法①:__________________________;
方法②:____________________________;
(2)根据(1)写出一个等式:__________________________.


(3)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.
试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
参考答案:
【答案】(1)①![]() ②
②![]() ;(2)
;(2)![]() =
=![]() ;(3)见解析
;(3)见解析
【解析】
第一问,可以把阴影部分面积看作一个小正方形或者大正方形减去四个矩形;第二问,直接由第一问建立等式;第三问,根据等式可以看出图形由两个大正方形、两个小正方形和五个小矩形构成一个大的矩形,试着画出图形即可.
(1)①![]() ;②小正方形面积可以看着大正方形面积减去4个长方形面积 ,即
;②小正方形面积可以看着大正方形面积减去4个长方形面积 ,即![]() ;
;
(2)由(1)正方形的面积有两种表示方法,所以![]() =
=![]() ;
;
(3)如图,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )

A. 14cm B. 17cm C. 20cm D. 23cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在计算3(4+1)(42+1)时,把3写成(4﹣1)后,发现可以连续运用平方差公式计算:3(4+1)(42+1)=(4﹣1)(4+1)(42+1)=(42﹣1)(42+1)=(42)2﹣12=256﹣1=255.请借鉴该同学的方法计算(2+1)(22+1)(24+1)(28+1)…(22048+1)=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
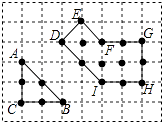
查看答案和解析>>【题目】在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中三角形ABC是格点三角形,其中S=2,N=0,L=6;图中格点多边形DEFGHI所对应的S,N,L分别是 . 经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S= . (用数值作答)
相关试题

