【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在 ![]() 上且不与A点重合,但Q点可与B点重合.
上且不与A点重合,但Q点可与B点重合. 
发现: ![]() 的长与
的长与 ![]() 的长之和为定值l,求l:
的长之和为定值l,求l:
参考答案:
【答案】解:如图1,连接OP、OQ, 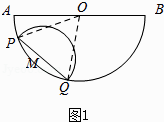
∵AB=4,
∴OP=OQ=2,
∵PQ=2,
∴△OPQ是等边三角形,
∴∠POQ=60°,
∴ ![]() =
= ![]() =
= ![]() ,
,
又∵半圆O的长为: ![]() π×4=2π,
π×4=2π,
∴ ![]() +
+ ![]() =2π﹣
=2π﹣ ![]() π=
π= ![]() ,
,
∴l= ![]() π;
π;
思考:点M与AB的最大距离为 , 此时点P,A间的距离为 ;
点M与AB的最小距离为 , 此时半圆M的弧与AB所围成的封闭图形面积为 ;![]() |2||
|2|| ![]()
![]() ﹣
﹣ ![]()
探究:当半圆M与AB相切时,求 ![]() 的长.
的长.
(注:结果保留π,cos35°= ![]() ,cos55°=
,cos55°= ![]() )
)
解:当半圆M与AB相切时,
此时,MC=1,
如图4,当点C在线段OA上时,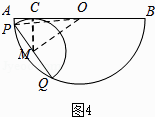
在Rt△OCM中,
由勾股定理可求得:OC= ![]() ,
,
∴cos∠AOM= ![]() =
= ![]() ,
,
∴∠AOM=35°,
∵∠POM=30°,
∴∠AOP=∠AOM﹣∠POM=5°,
∴ ![]() =
= ![]() =
= ![]() ,
,
当点C在线段OB上时,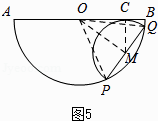
此时,∠BOM=35°,
∵∠POM=30°,
∴∠AOP=180°﹣∠POM﹣∠BOM=115°
∴ ![]() =
= ![]() =
= ![]() ,
,
综上所述,当半圆M与AB相切时, ![]() 的长为
的长为 ![]() 或
或 ![]() .
.
【解析】解:发现: 思考:如图2,过点M作MC⊥AB于点C,
连接OM,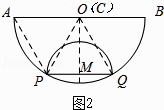
∵OP=2,PM=1,
∴由勾股定理可知:OM= ![]() ,
,
当C与O重合时,
M与AB的距离最大,最大值为 ![]() ,
,
连接AP,
此时,OM⊥AB,
∴∠AOP=60°,
∵OA=OP,
∴△AOP是等边三角形,
∴AP=2,
如图3,当Q与B重合时,
连接DM,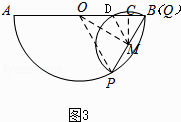
∵∠MOQ=30°,
∴MC= ![]() OM=
OM= ![]() ,
,
此时,M与AB的距离最小,最小值为 ![]() ,
,
设此时半圆M与AB交于点D,
DM=MB=1,
∵∠ABP=60°,
∴△DMB是等边三角形,
∴∠DMB=60°,
∴扇形DMB的面积为: ![]() =
= ![]() ,
,
△DMB的面积为: ![]() MCDB=
MCDB= ![]() ×
× ![]() ×1=
×1= ![]() ,
,
∴半圆M的弧与AB所围成的封闭图形面积为: ![]() ﹣
﹣ ![]() ;
;
-
科目: 来源: 题型:
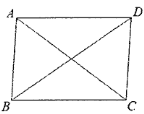
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,AC、BD是对角线,下列条件中能判定平行四边形ABCD为矩形的是()
A.
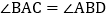 B.
B. 
C.
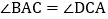 D.
D. 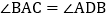
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
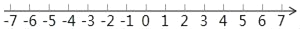
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小玲和小明值日打扫教室卫生,小玲单独打扫雪20min完成,小明单独打扫雪16min完成.因小明要将数学作业本交到老师办公室推迟一会儿,故先由小玲单独打扫4min,余下的再由两人一起完成,则两人一起打扫完教师卫生需要多长时间?设两人一起打扫完教室卫生需要x min,则根据题意可列方程( )
A.
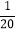 (x+4)+
(x+4)+ x=1 B.
x=1 B. 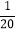 x+
x+ (x+4)=1
(x+4)=1C.
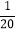 (x﹣4)+
(x﹣4)+ x=1 D.
x=1 D. 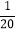 x+
x+ (x﹣4)=1
(x﹣4)=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展
 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:组别
个人年消费金额
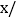 元
元频数
频率
A
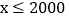
18

B

a
b
C
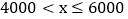
D
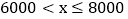
24
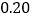
E
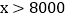
12

合计
c
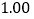

根据以上信息解答下列问题:
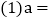 ________;
________;  ________;
________; 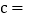 ________;
________; 补全频数分布直方图;
补全频数分布直方图;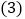 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度
投入技改资金
 万元
万元产品成本
 万元
万元 件
件
2014


2015
3
12
2016
4
9
2017

8
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,直接写出y与x的函数关系式;
(2)按照这种变化规律,若2018年已投入资金6万元.
①预计2018年每件产品成本比2017年降低多少万元?
②若计划在2018年把每件产品成本降低到5万元,则还需要投入技改资金多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:像
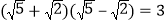 、
、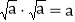
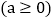 、
、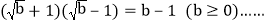 两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式 例如,
例如,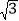 与
与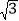 、
、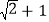 与
与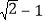 、
、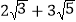 与
与 等都是互为有理化因式
等都是互为有理化因式 在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.例如;
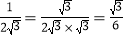 ;
;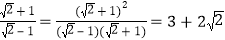 .
.解答下列问题:
(1)
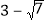 与________互为有理化因式,将
与________互为有理化因式,将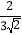 分母有理化得________;
分母有理化得________;(2)计算:
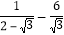 ;
;(3)己知有理数a、b满足
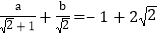 ,求a、b的值.
,求a、b的值.
相关试题

