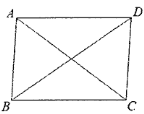
【题目】如图,已知四边形ABCD是平行四边形,AC、BD是对角线,下列条件中能判定平行四边形ABCD为矩形的是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形;(3)对角线相等的平行四边形是矩形.据此分析判断.
A、∵∠BAC=∠ABD,∴OA=OB,∴AC=BD,能判定平行四边形ABCD为矩形,正确;
B、∵∠BAC=∠DAC,BO=OD,∴AB=AD,能判定平行四边形ABCD为菱形,错误;
C、∵∠BAC=∠DCA,∴AB∥CD,不能判定平行四边形ABCD为矩形,错误;
D、∵∠BAC=∠ADB,不能判定平行四边形ABCD为矩形,错误;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数
第一次
第二次
第三次
第四次
行驶情况
x
﹣
 x
xx﹣3
2(5﹣x)
行驶方向(填“东”或“西”)
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
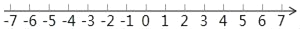
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小玲和小明值日打扫教室卫生,小玲单独打扫雪20min完成,小明单独打扫雪16min完成.因小明要将数学作业本交到老师办公室推迟一会儿,故先由小玲单独打扫4min,余下的再由两人一起完成,则两人一起打扫完教师卫生需要多长时间?设两人一起打扫完教室卫生需要x min,则根据题意可列方程( )
A.
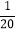 (x+4)+
(x+4)+ x=1 B.
x=1 B. 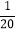 x+
x+ (x+4)=1
(x+4)=1C.
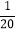 (x﹣4)+
(x﹣4)+ x=1 D.
x=1 D. 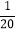 x+
x+ (x﹣4)=1
(x﹣4)=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在
 上且不与A点重合,但Q点可与B点重合.
上且不与A点重合,但Q点可与B点重合. 
发现: 的长与
的长与  的长之和为定值l,求l:
的长之和为定值l,求l:
相关试题

