搜索
【题目】阅读材料：像
、
、
两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式
例如，
与、
与
、
与
等都是互为有理化因式在进行二次根式计算时，利用有理化因式，可以化去分母中的根号．
例如；
；
．
解答下列问题：
（1）
与________互为有理化因式，将
分母有理化得________；
（2）计算：
；
（3）己知有理数a、b满足
，求a、b的值．
参考答案：
【答案】
；
；
，
．
【解析】（1）根据题意可以得到所求式子的分母有理化因式，并将题目中的二次根式化简；
（2）根据分母有理化的方法可以化简题目中的式子；
（3）根据题意，对所求式子变形即可求得a、b的值．
（1）
与
互为有理化因式，
，
故答案为；；
原式
；
，
，
，
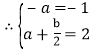解这个方程组，得：
，
，．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，半圆O的直径AB=4，以长为2的弦PQ为直径，向点O方向作半圆M，其中P点在
上且不与A点重合，但Q点可与B点重合． 
发现：
的长与 
的长之和为定值l，求l： -
科目： 来源： 题型：
查看答案和解析>>【题目】随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
随机抽取部分员工，记录每个人年消费金额，并将调查数据适当整理，绘制成如下两幅尚不完整的表和图：组别
个人年消费金额
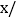元频数
频率
A
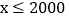
18
B
a
b
C
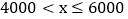
D
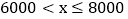
24
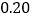
E
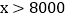
12
合计
c
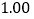
根据以上信息解答下列问题：
________； 
________； 
________；
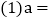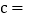补全频数分布直方图；
若这个企业有3000名员工，请你估计个人旅游年消费金额在6000元以上的人数． -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：
年度
投入技改资金
万元产品成本
万元
件
2014
2015
3
12
2016
4
9
2017
8
（1）分析表中数据，请从一次函数和反比例函数中确定一个函数表示其变化规律，直接写出y与x的函数关系式；
（2）按照这种变化规律，若2018年已投入资金6万元．
①预计2018年每件产品成本比2017年降低多少万元？
②若计划在2018年把每件产品成本降低到5万元，则还需要投入技改资金多少万元？
-
科目： 来源： 题型：
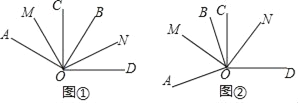
查看答案和解析>>【题目】如图①，∠AOB=∠COD=90°，OM平分∠AOC，ON平分∠BOD．
（1）已知∠BOC=20°，且∠AOD小于平角，求∠MON的度数；
（2）若（1）中∠BOC=α，其它条件不变，求∠MON的度数；
（3）如图②，若∠BOC=α，且∠AOD大于平角，其它条件不变，求∠MON的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设抛物线的解析式为y=ax2 ， 过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点B2（
，0）作x轴的垂线，交抛物线于点A2；…；过点Bn（（ ）n﹣1 ， 0）（n为正整数）作x轴的垂线，交抛物线于点An ， 连接AnBn+1 ， 得Rt△AnBnBn+1 ．
（1）求a的值；
（2）直接写出线段AnBn ， BnBn+1的长（用含n的式子表示）；
（3）在系列Rt△AnBnBn+1中，探究下列问题：
①当n为何值时，Rt△AnBnBn+1是等腰直角三角形？
②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似？若存在，求出其相似比；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两支“徒步队”到野外沿相同路线徒步，徒步的路程为24千米．甲队步行速度为4千米/时，乙队步行速度为6千米/时．甲队出发1小时后，乙队才出发，同时乙队派一名联络员跑步在两队之间来回进行一次联络（不停顿），他跑步的速度为10千米/时．
（1）乙队追上甲队需要多长时间？
（2）联络员从出发到与甲队联系上后返回乙队时，他跑步的总路程是多少？
（3）从甲队出发开始到乙队完成徒步路程时止，何时两队间间隔的路程为1千米？
相关试题
