【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点,A点坐标为(﹣1,0).
经过A,B两点,A点坐标为(﹣1,0).
(1)求B、C两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.

参考答案:
【答案】(1)B(3,0),C(0, ![]() );(2)y=﹣
);(2)y=﹣![]() x2+
x2+![]() x+
x+![]() ;(3)
;(3)![]()
【解析】试题分析:(1)分别令x,y得零,求坐标.(2)利用待定系数法求二次函数解析式.(3)建立△DMH二次函数关系,求最值即可.
试题解析:
(1)∵直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0, ![]() );
);
(2)∵抛物线y=ax2+bx+![]() 经过A,B两点,
经过A,B两点,
∴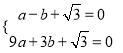 ,
,
解得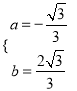 .
.
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+
x+![]()
(3)∵B(3,0),C(0, ![]() );
);
∴OB=3,OC=![]() ,
,
∴tan∠BCO=![]() ,
,
∴∠BCO=60°,
∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH=![]() DM,MH=
DM,MH=![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+![]() DM+
DM+![]() DM=
DM=![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣ ![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ﹣(﹣
﹣(﹣![]() t+
t+![]() )=﹣
)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为![]() ,
,
此时![]() DM=
DM=![]() ,
,
即△DMH周长的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=
 ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.(1)求直线l的表达式;
(2)若反比例函数
 的图象经过点P,求m的值.
的图象经过点P,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(﹣2.4)+(﹣3.7)+(﹣4.6)+5.7
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)

(4)(﹣3
 )+12.5+(16
)+12.5+(16 )﹣(﹣2.5)
)﹣(﹣2.5)(5)0.75+0.125+(﹣2
 )﹣(﹣12
)﹣(﹣12 )+(﹣4
)+(﹣4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减(辆)
-1
+3
-2
-4
+7
-5
-10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
-
科目: 来源: 题型:
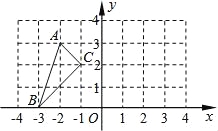
查看答案和解析>>【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子摆成的“
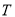 ”字形图,如图所示:
”字形图,如图所示: ……
……(1)填写下表:
图案序号
①
②
③
④
…
⑩
每个图案中棋子的个数
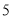

______
_____
…
______
(2)写出第
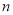 个“
个“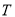 ”字形图案中棋子的个数(用含
”字形图案中棋子的个数(用含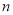 的代数式表示):
的代数式表示):(3)第20个“
 ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
相关试题

