【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=![]() ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.
(1)求直线l的表达式;
(2)若反比例函数![]() 的图象经过点P,求m的值.
的图象经过点P,求m的值.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)已知A(2,0)an∠OAB=![]() =
=![]() ,可求得OB=1,所以B(0,1),设直线l的表达式为
,可求得OB=1,所以B(0,1),设直线l的表达式为![]() ,用待定系数法即可求得直线l的表达式;(2)根据直线l上的点P位于y轴左侧,且到y轴的距离为1可得点P的横坐标为-1,代入一次函数的解析式求得点P的纵坐标,把点P的坐标代入反比例函数
,用待定系数法即可求得直线l的表达式;(2)根据直线l上的点P位于y轴左侧,且到y轴的距离为1可得点P的横坐标为-1,代入一次函数的解析式求得点P的纵坐标,把点P的坐标代入反比例函数![]() 中,即可求得m的值.
中,即可求得m的值.
试题解析:(1) ∵A(2,0),∴OA=2.
∵tan∠OAB=![]() =
=![]() ,
,
∴OB="1." ∴B(0,1).
设直线l的表达式为![]() ,则
,则
![]()
∴![]() .
.
∴直线l的表达式为![]() .
.
(2) ∵点P到y轴的距离为1,且点P在y轴左侧,
∴点P的横坐标为-1.
又∵点P在直线l上,
∴点P的纵坐标为: ![]() .
.
∴点P的坐标是![]() .
.
∵反比例函数![]() 的图象经过点P,
的图象经过点P,
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),将△ABC向右平移5个单位长度,再向上平移3个单位长度得到△
 ,其中点
,其中点  分别是点A,B,C的对应点.
分别是点A,B,C的对应点.(1)请你在给出的坐标系中画出
 和写出点A′,C′的坐标;
和写出点A′,C′的坐标;(2)若△ABC内的一点P经过上述平移后的对应点为
 ,用含
,用含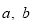 的式子表示P点的坐标 ;(直接写出结果即可)
的式子表示P点的坐标 ;(直接写出结果即可)(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是按照一定规律画出的一列“树型”图:

经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出_____个“树枝”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x
30
32
34
36
y
40
36
32
28
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(﹣2.4)+(﹣3.7)+(﹣4.6)+5.7
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)

(4)(﹣3
 )+12.5+(16
)+12.5+(16 )﹣(﹣2.5)
)﹣(﹣2.5)(5)0.75+0.125+(﹣2
 )﹣(﹣12
)﹣(﹣12 )+(﹣4
)+(﹣4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+ 分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+ 经过A,B两点,A点坐标为(﹣1,0).
经过A,B两点,A点坐标为(﹣1,0).(1)求B、C两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.

相关试题

