【题目】定义正整数m,n的运算,m△n=![]()
例2△3=![]() ,3△4=
,3△4=![]()
(1)3△2的值为 运算符号“△”满足交换律吗?回答 (填“是”或者“否”)
(2)探究:计算2△10=![]() 的值.
的值.
为解决上面的问题,我们运用数形结合的思想方法,通过不断的分割一个面积为1的正方形,把数量关系和几何图形结合起来,最终解决问题.
如图所示,第1次分割把正方形的面积二等分,其中阴影部分的面积为![]() ,第2次,把上次分割图中空白部分的面积继续二等分,阴影分的面积之和为
,第2次,把上次分割图中空白部分的面积继续二等分,阴影分的面积之和为![]() ,第3次分割把上次分割图中空白部分的面积继续二等分……以此类推……第10次分割,把第9次分割后的图中的空日部分的面积最后二等分,所有阴影部分面积之和为
,第3次分割把上次分割图中空白部分的面积继续二等分……以此类推……第10次分割,把第9次分割后的图中的空日部分的面积最后二等分,所有阴影部分面积之和为![]() .
.
根据第10次分割图可以得出计结果:![]() =1﹣
=1﹣![]() ,进一步分析可得出
,进一步分析可得出![]() =1﹣
=1﹣![]() ,
,

(3)已知n是正整数,计算3×(4△n)=![]() 的结果.
的结果.
按指定方法解决问题请仿照以上做法,只需画出第n次分割图并作标注,写出最终结果的推理步骤,或借用以上结论进行推理,写出必要的步骤.
参考答案:
【答案】(1)![]() ,否(2)1-
,否(2)1-![]() (3)见解析
(3)见解析
【解析】
(1)根据新定义运算法则进行计算即可;重点是理解新定义是如何运算的
(2)根据计算2△10=…+ ![]() 的值的计算过程得到规律解题;
的值的计算过程得到规律解题;
(3)根据探究的分割方法依次进行分割,然后表示出阴影部分的面积,再除以3即可.
(1)3△2=![]() ,而2△3=
,而2△3=![]() ,则3△2≠2△3,
,则3△2≠2△3,
所以运算“△”不满足交换规律
故答案是:![]() ;否;
;否;
(2)如图所示,第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积这和为![]() ;
;
第3次分割,把上次图中空白部分的面积继续二等分,…依此类推,…
第10次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() ,最后空白部分的面积为
,最后空白部分的面积为![]() ;
;
根据第10次分割图可以得出计算结果为![]() ;
;
进一步分析可得出:果为![]() ;
;
故答案是:1﹣![]() .
.
(3)第1次分割,把正方形的面积四等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续四等分,阴影部分的面积为![]() ;
;
第3次分害,把上次分割图中空白部分的面积继续四等分,阴影部分的面积……,
第n次分害,把上次分割图中空白部分的面积继续四等分,阴影部分的面积
![]() ,最后的空白部分的面积是
,最后的空白部分的面积是![]() ;
;
根据第n次公害图可得等式:![]() .
.
两边同除以3,得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点F在ABCD的对角线AC上,过点F,B分别作AB,AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.

(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE= ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018密云生态半程马拉松于6月10日鸣枪开跑.本届赛事设有半程马拉松和迷你马拉松两个参赛项目,涉及参赛选手5000人;另外,还有将近1200名医护和社会志愿者参与本届大赛的志愿服务活动.请你用科学记数法表示参加本届赛事的所有参赛选手和志愿者的总人数为( )
A.
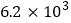 B.
B. 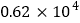 C.
C. 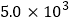 D.
D. 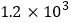
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____.

相关试题

