【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
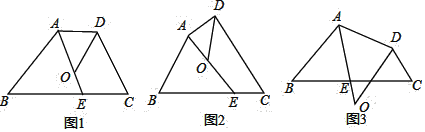
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
参考答案:
【答案】(1)①125;②∠B+∠C+2∠DOE=360°,理由详见解析;(2)∠B+∠C=2∠DOE,理由详见解析.
【解析】
(1)①根据平行线的性质和角平分线的定义可求∠BAE,∠CDO,再根据三角形外角的性质可求∠AEC,再根据四边形内角和等于360°可求∠DOE的度数;
②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系,再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系;
(2)根据四边形和三角形的内角和得到∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,根据角平分线的定义得到∠BAD=2∠EAD,∠ADC=2∠ADO,于是得到结论.
解:(1)①∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案为:125;
②∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分别平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°;
(2)∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.
-
科目: 来源: 题型:
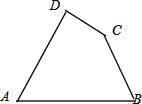
查看答案和解析>>【题目】如图,四边形ABCD是一个工件的平面图,它要求AD和BC这两边的夹角应等于30°.甲、乙、丙三个工人在检验工件是否合格时,发生了以下争论:
甲:要检验工件是否合格,应延长AD和BC,设交点为O,然后检验∠O是否等于30°.
乙:这样太麻烦了,我看只需测量出∠A和∠B的度数就行了.
丙:量出∠C和∠D的度数也可以检验AD和BC的夹角是否等于30°.
请你用所学过的知识,说明乙、丙两人的方法是否正确.
-
科目: 来源: 题型:
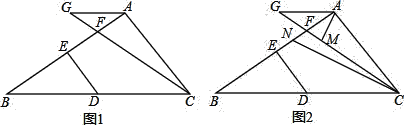
查看答案和解析>>【题目】已知,在三角形ABC中,点D在BC上,DE⊥AB于E,点F在AB上,在CF的延长线上取一点G,连接AG.
(1)如图1,若∠GAB=∠B,∠GAC+∠EDB=180°,求证:AB⊥AC.
(2)如图2.在(1)的条件下,∠GAC的平分线交CG于点M,∠ACB的平分线交AB于点N,当∠AMC-∠ANC=35°时,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径作弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE.若AB=6,BC=8,则△ABE的周长为 .
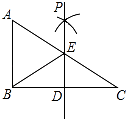
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC外作射线AD,使得AD和AC在直线AB的两侧,∠BAD=α(0°<α<180°),点B关于直线AD的对称点为P,连接PB,PC.
(1)依题意补全图1;
(2)在图1中,求△BPC的度数;
(3)直接写出使得△PBC是等腰三角形的α的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料
小明遇到这样一个问题:求计算
 所得多项式的一次项系数.
所得多项式的一次项系数.小明想通过计算
 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.他决定从简单情况开始,先找
 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
也就是说,只需用
 中的一次项系数1乘以
中的一次项系数1乘以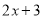 中的常数项3,再用
中的常数项3,再用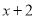 中的常数项2乘以
中的常数项2乘以 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加 ,即可得到一次项系数.
,即可得到一次项系数.延续上面的方法,求计算
 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用 的一次项系数1,
的一次项系数1,  的常数项3,
的常数项3,  的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用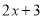 的一次项系数2,
的一次项系数2,  的常数项2,
的常数项2,  的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用 的一次项系数3,
的一次项系数3,  的常数项2,
的常数项2,  的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题:
(1)计算
 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .(2)计算
 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .(3)若计算
 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则 =_________.
=_________.(4)若
 是
是 的一个因式,则
的一个因式,则 的值为 .
的值为 .
相关试题

