【题目】如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( ) 
A.40°
B.60°
C.70°
D.80°
参考答案:
【答案】D
【解析】解:∵四边形ABCD是圆内接四边形, ∴∠ADC+∠B=180°,又∠ADC=140°,
∴∠B=40°,
∴∠AOC=2∠B=80°,
故选:D.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对圆内接四边形的性质的理解,了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.
,求AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,求:
,求:①A–3B;②3A+B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
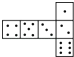 B.
B.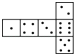 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )

A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP?AC
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN=
 ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
相关试题

