【题目】已知![]() ,
,![]() ,求:
,求:
①A–3B;②3A+B.
参考答案:
【答案】(1) x2–7xy+16y2;(2) 13x2–11xy–2y2.
【解析】
(1)列出A-3B的式子,再去括号,合并同类项即可;
(2)列出3A+B的式子,再去括号,合并同类项即可.
解:(1)∵A=4x2-4xy+y2,B=x2+xy-5y2,
∴A-3B=(4x2-4xy+y2)-3(x2+xy-5y2)
=4x2-4xy+y2-3x2-3xy+15y2
=(4-3)x2-(4+3)xy+(1+15)y2
=x2-7xy+16y2;
(2)∵A=4x2-4xy+y2,B=x2+xy-5y2,
∴3A+B=3(4x2-4xy+y2)+(x2+xy-5y2)
=12x2-12xy+3y2+x2+xy-5y2
=(12+1)x2-(12-1)xy+(3-5)y2
=13x2-11xy-2y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)

(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.

(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.
,求AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
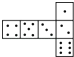 B.
B.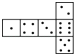 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )

A.40°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )

A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP?AC
D.
相关试题

