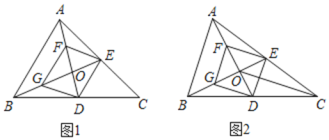
【题目】如图,在![]() 中,点D,E分别是边BC,AC的中点,AD与BE相交于点
中,点D,E分别是边BC,AC的中点,AD与BE相交于点![]() 点F,G分别是线段AO,
点F,G分别是线段AO,
BO的中点.
![]() 求证:四边形DEFG是平行四边形;
求证:四边形DEFG是平行四边形;
![]() 如图2,连接CO,若
如图2,连接CO,若![]() ,求证:四边形DEFG是菱形;
,求证:四边形DEFG是菱形;
![]() 在
在![]() 的前提下,当
的前提下,当![]() 满足什么条件时,四边形DEFG能成为正方形?
满足什么条件时,四边形DEFG能成为正方形?![]() 直接回答即可,不必证明
直接回答即可,不必证明![]()
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)由三角形中位线性质得到![]() ,
,![]() ,故四边形DEFG是平行四边形;(2)同(1),由
,故四边形DEFG是平行四边形;(2)同(1),由![]() ,证
,证![]() ,得到菱形;(3)当
,得到菱形;(3)当![]() 时,四边形DEFG为正方形:点D,E分别是边BC,AC的中点,得点O是
时,四边形DEFG为正方形:点D,E分别是边BC,AC的中点,得点O是![]() 的重心,证
的重心,证![]() ,
,![]() ,结合平行线性质证
,结合平行线性质证![]() ,结合(2)可得结论.
,结合(2)可得结论.
![]() 证明:
证明:![]() 点D,E分别是边BC,AC的中点,
点D,E分别是边BC,AC的中点,![]() ,
,![]() ,
,![]() 点F,G分别是线段AO,BO的中点,
点F,G分别是线段AO,BO的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 四边形DEFG是平行四边形;
四边形DEFG是平行四边形;![]() 证明:
证明:![]() 点F,E分别是边OA,AC的中点,
点F,E分别是边OA,AC的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平行四边形DEFG是菱形;
平行四边形DEFG是菱形;![]() 当
当![]() 时,四边形DEFG为正方形,
时,四边形DEFG为正方形,
理由如下:![]() 点D,E分别是边BC,AC的中点,
点D,E分别是边BC,AC的中点,![]() 点O是
点O是![]() 的重心,
的重心,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 菱形DEFG为正方形.
菱形DEFG为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力
科研能力
组织能力
甲
81
85
86
乙
92
80
74
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某河道A,B两个码头之间有客轮和货轮通行
 一天,客轮从A码头匀速行驶到B码头,同时货轮从
一天,客轮从A码头匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头
 两船距B码头的距离
两船距B码头的距离 千米
千米 与行驶时间
与行驶时间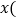 分
分 之间的函数关系
之间的函数关系如图所示
 请根据图象解决下列问题:
请根据图象解决下列问题: 分别求客轮和货轮距B码头的距离
分别求客轮和货轮距B码头的距离 千米
千米 、
、 千米
千米 与
与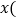 分
分 之间的函数关系式;
之间的函数关系式; 求点M的坐标,并写出该点坐标表示的实际意义.
求点M的坐标,并写出该点坐标表示的实际意义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置
 已知
已知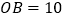 ,
, ,将这张纸片沿过点B的直
,将这张纸片沿过点B的直线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
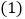 点C的坐标为______;
点C的坐标为______; 求点E的坐标及直线BE的函数关系式;
求点E的坐标及直线BE的函数关系式; 若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?若存在,直接写出相应的点Q的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象不经过第四象限
-
科目: 来源: 题型:
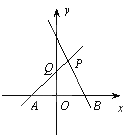
查看答案和解析>>【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
相关试题

