【题目】问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置![]() 已知
已知![]() ,
,![]() ,将这张纸片沿过点B的直
,将这张纸片沿过点B的直
线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
![]() 点C的坐标为______;
点C的坐标为______;
![]() 求点E的坐标及直线BE的函数关系式;
求点E的坐标及直线BE的函数关系式;
![]() 若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若存在,直接写出相应的点Q的坐标;若不存在,说明理由.

参考答案:
【答案】(1)(10,6);(2)![]() ),
),![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据矩形性质可得到C的坐标;(2)设![]() ,由折叠知,
,由折叠知,![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,即
,即![]() ,解得
,解得![]() ,可得
,可得![]() ;由待定系数法可求直线BE的解析式;(3)存在,理由:由
;由待定系数法可求直线BE的解析式;(3)存在,理由:由![]() 知,
知,![]() ,
,![]() ,设
,设![]() ,分两种情况分析:
,分两种情况分析:![]() 当BQ为的对角线时;
当BQ为的对角线时;![]() 当BQ为边时.
当BQ为边时.
解:![]() 四边形OBCD是矩形,
四边形OBCD是矩形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故答案为:![]() ;
;![]() 四边形OBCD是矩形,
四边形OBCD是矩形,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
由折叠知,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设直线BE的函数关系式为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 直线BE的函数关系式为
直线BE的函数关系式为![]() ;
;![]() 存在,理由:由
存在,理由:由![]() 知,
知,![]() ,
,![]() ,
,![]() 能使以A,B,P,Q为顶点的四边形是平行四边形,
能使以A,B,P,Q为顶点的四边形是平行四边形,![]() ,
,![]() 当BQ为的对角线时,
当BQ为的对角线时,![]() ,
,![]() 点B,P在x轴,
点B,P在x轴,![]() 的纵坐标等于点A的纵坐标6,
的纵坐标等于点A的纵坐标6,![]() 点Q在直线BE:
点Q在直线BE:![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 当BQ为边时,
当BQ为边时,![]() 与BP互相平分,
与BP互相平分,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
即:直线BE上是存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形,点![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某河道A,B两个码头之间有客轮和货轮通行
 一天,客轮从A码头匀速行驶到B码头,同时货轮从
一天,客轮从A码头匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头
 两船距B码头的距离
两船距B码头的距离 千米
千米 与行驶时间
与行驶时间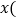 分
分 之间的函数关系
之间的函数关系如图所示
 请根据图象解决下列问题:
请根据图象解决下列问题: 分别求客轮和货轮距B码头的距离
分别求客轮和货轮距B码头的距离 千米
千米 、
、 千米
千米 与
与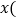 分
分 之间的函数关系式;
之间的函数关系式; 求点M的坐标,并写出该点坐标表示的实际意义.
求点M的坐标,并写出该点坐标表示的实际意义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
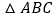 中,点D,E分别是边BC,AC的中点,AD与BE相交于点
中,点D,E分别是边BC,AC的中点,AD与BE相交于点 点F,G分别是线段AO,
点F,G分别是线段AO,BO的中点.
 求证:四边形DEFG是平行四边形;
求证:四边形DEFG是平行四边形;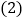 如图2,连接CO,若
如图2,连接CO,若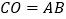 ,求证:四边形DEFG是菱形;
,求证:四边形DEFG是菱形;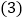 在
在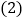 的前提下,当
的前提下,当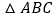 满足什么条件时,四边形DEFG能成为正方形?
满足什么条件时,四边形DEFG能成为正方形?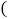 直接回答即可,不必证明
直接回答即可,不必证明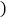
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象不经过第四象限
-
科目: 来源: 题型:
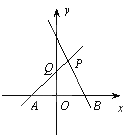
查看答案和解析>>【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
相关试题

