【题目】![]() 如图
如图![]() 所示,在
所示,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() 的周长
的周长![]() ;21.
;21.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.


参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:![]() 由直线
由直线![]() 为线段
为线段![]() 的垂直平分线,根据线段垂直平分线定理:可得
的垂直平分线,根据线段垂直平分线定理:可得![]() ,同理可得
,同理可得![]() ,然后表示出三角形
,然后表示出三角形![]() 的三边之和,等量代换可得其周长等于
的三边之和,等量代换可得其周长等于![]() 的长;
的长;
![]() 由
由![]() ,可得
,可得![]() ,又由
,又由![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于
于![]() ,得出
,得出![]() ,即可得出
,即可得出![]() ,同理:
,同理:![]() ,即可得出结论;
,即可得出结论;
![]() 先利用
先利用![]() 是
是![]() 垂直平分线计算出
垂直平分线计算出![]() ,进而得出
,进而得出![]() ,进而得出
,进而得出![]() ,最后用勾股定理即可得出结论.
,最后用勾股定理即可得出结论.
试题解析:![]() ∵直线
∵直线![]() 为线段
为线段![]() 的垂直平分线(已知),
的垂直平分线(已知),
∴![]() (线段垂直平分线上的点到线段两端点的距离相等),
(线段垂直平分线上的点到线段两端点的距离相等),
又直线![]() 为线段
为线段![]() 的垂直平分线(已知),
的垂直平分线(已知),
∴![]() (线段垂直平分线上的点到线段两端点的距离相等),
(线段垂直平分线上的点到线段两端点的距离相等),
∴![]() 的周长
的周长![]() (等量代换);
(等量代换);
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
![]() ∵
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
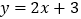 与直线
与直线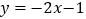 .
.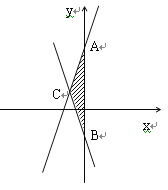
【1】(1)求两直线与
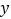 轴交点A,B的坐标;
轴交点A,B的坐标;【2】(2)求两直线交点C的坐标;
【3】(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程
 (米)与时间
(米)与时间 (分钟)之间的函数图象如图所示,根据图象回答下列问题:
(分钟)之间的函数图象如图所示,根据图象回答下列问题:
 最先达到终点的是________队,比另一对早________分钟到达;
最先达到终点的是________队,比另一对早________分钟到达; 在比赛过程中,乙队在第________分钟和第________分钟时两次加速;
在比赛过程中,乙队在第________分钟和第________分钟时两次加速; 求在什么时间范围内,甲队领先?
求在什么时间范围内,甲队领先? 相遇前,甲乙两队之间的距离不超过
相遇前,甲乙两队之间的距离不超过 的时间范围是________.
的时间范围是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.

∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC内接于⊙O,过点A作直线EF.

(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:

(1)该种软件上市第几个月后开始盈利?
(2)求累积利润S(万元)与时间t(月)之间的函数表达式;
(3)截止到几月末,公司累积利润达到30万元?
(4)求公司第6个月末所累积的利润.
相关试题

