【题目】百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数图象如图所示,根据图象回答下列问题:
(分钟)之间的函数图象如图所示,根据图象回答下列问题:

![]() 最先达到终点的是________队,比另一对早________分钟到达;
最先达到终点的是________队,比另一对早________分钟到达;
![]() 在比赛过程中,乙队在第________分钟和第________分钟时两次加速;
在比赛过程中,乙队在第________分钟和第________分钟时两次加速;
![]() 求在什么时间范围内,甲队领先?
求在什么时间范围内,甲队领先?
![]() 相遇前,甲乙两队之间的距离不超过
相遇前,甲乙两队之间的距离不超过![]() 的时间范围是________.
的时间范围是________.
参考答案:
【答案】 乙 0.6 1 3 ![]() 或
或![]()
【解析】试题分析:![]() 根据函数图象可以直接得到谁先到达终点和早到多长时间;
根据函数图象可以直接得到谁先到达终点和早到多长时间;
![]() 根据函数图象可以得到乙队在第几分钟开始加速;
根据函数图象可以得到乙队在第几分钟开始加速;
![]() 根据函数图象可以去的甲乙对应的函数解析式,从而可以得到在什么时间范围内,甲队领先;
根据函数图象可以去的甲乙对应的函数解析式,从而可以得到在什么时间范围内,甲队领先;
![]() 根据函数图象可以求得相遇前,甲乙两队之间的距离不超过
根据函数图象可以求得相遇前,甲乙两队之间的距离不超过![]() 的时间范围.
的时间范围.
试题解析:![]() 由图象可得,最先达到终点的是乙队,比甲队早到:
由图象可得,最先达到终点的是乙队,比甲队早到:![]() 分钟;
分钟;
![]() 由图象可得,在比赛过程中,乙队在第
由图象可得,在比赛过程中,乙队在第![]() 分钟和第
分钟和第![]() 分钟时两次加速,
分钟时两次加速,
(3)设甲队对应的函数解析式为![]() ,
,
![]() ,得
,得![]() ,
,
即甲队对应的函数解析式为![]() ,
,
当![]() 时,乙队对应的函数解析式为
时,乙队对应的函数解析式为![]() ,
,
![]() ,得
,得![]() ,
,
即当![]() 时,乙队对应的函数解析式为
时,乙队对应的函数解析式为![]() ,
,
令![]() ,得
,得![]() ,
,
即当![]() 时,甲队领先;
时,甲队领先;
![]() 当
当![]() 时,设乙对应的函数解析式为
时,设乙对应的函数解析式为![]() ,
,
![]() ,
,
即当![]() 时,乙对应的函数解析式为
时,乙对应的函数解析式为![]() ,
,
![]() ,
,
解得,![]() ,
,
即当![]() 时,甲乙两队之间的距离不超过
时,甲乙两队之间的距离不超过![]() ,
,
当![]() 时,设乙队对应的函数解析式为
时,设乙队对应的函数解析式为![]() ,
,
![]() ,得
,得![]() ,
,
当![]() 时,乙队对应的函数解析式为
时,乙队对应的函数解析式为![]() ,
,
![]() ,得
,得![]() (舍去),
(舍去),
乙在![]() 段对应的函数解析式为
段对应的函数解析式为![]() ,
,
则![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
由上可得,当![]() 或
或![]() 时,甲乙两队之间的距离不超过
时,甲乙两队之间的距离不超过![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.

(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
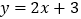 与直线
与直线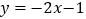 .
.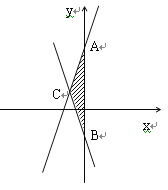
【1】(1)求两直线与
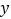 轴交点A,B的坐标;
轴交点A,B的坐标;【2】(2)求两直线交点C的坐标;
【3】(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 如图
如图 所示,在
所示,在 中,
中, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 .
. 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 、
、 ,求证:
,求证: 的周长
的周长 ;21.
;21. 如图
如图 所示,在
所示,在 中,若
中,若 ,
, ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 .
. 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 、
、 ,试判断
,试判断 的形状,并证明你的结论.
的形状,并证明你的结论. 如图
如图 所示,在
所示,在 中,若
中,若 ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 、
、 ,若
,若 ,
, ,求
,求 的长.
的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.

∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC内接于⊙O,过点A作直线EF.

(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.
相关试题

